题目内容
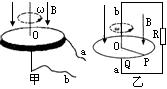 圆盘发电机的构造如图甲水平放置的金属圆盘在竖直向下的匀强磁场中绕与圆盘平面垂直且过圆盘中心O点的轴匀速转动,从a、b两端将有电压输出。现将此发电机简化成如图乙所示的模型:固定的金属圆环水平放置,金属棒OP绕圆环中心O以角速度
圆盘发电机的构造如图甲水平放置的金属圆盘在竖直向下的匀强磁场中绕与圆盘平面垂直且过圆盘中心O点的轴匀速转动,从a、b两端将有电压输出。现将此发电机简化成如图乙所示的模型:固定的金属圆环水平放置,金属棒OP绕圆环中心O以角速度![]() 匀速转动,金属棒的P端与圆环无摩擦紧密接触,整个装置放在竖直向下的匀强磁场中。已知圆环半径OP = 20 cm,圆环总电阻为R1 = 0.4
匀速转动,金属棒的P端与圆环无摩擦紧密接触,整个装置放在竖直向下的匀强磁场中。已知圆环半径OP = 20 cm,圆环总电阻为R1 = 0.4![]() ,金属棒的电阻R2 = 0.1
,金属棒的电阻R2 = 0.1![]() ,金属棒转动的角速度为
,金属棒转动的角速度为![]() = 500 rad/s,磁感应强度B = 1 T,外接负载电阻R = 0.3
= 500 rad/s,磁感应强度B = 1 T,外接负载电阻R = 0.3![]() 。求:
。求:
(1)金属棒OP中产生的感应电动势的大小为多少?O、P两点哪点电势高?
(2)负载电阻上的最大功率与最小功率各为多少?
(1)金属棒OP产生的感应电动势为:E = BL![]() ,代入数据得E = 10 V。根据右手定则可判断感应电流的方向为P→O,所以O点电势高。
,代入数据得E = 10 V。根据右手定则可判断感应电流的方向为P→O,所以O点电势高。
(2)电阻R上消耗的最大功率为P1 = I12R = 187.5 W。
电阻R上消耗的最小功率为P2 = I22R = 120 W。
解析:
(1)金属棒OP产生的感应电动势为:E = BL![]() ,代入数据得E = 10 V。根据右手定则可判断感应电流的方向为P→O,所以O点电势高。
,代入数据得E = 10 V。根据右手定则可判断感应电流的方向为P→O,所以O点电势高。
(2)当P点与Q点重合时,电路中的总电阻最小,R总= R + R2 = (0.1 + 0.3)![]() = 0.4
= 0.4![]() ,电路中的总电流最大,其最大值为I1 = E/R总= 10/0.4 A = 25 A,则电阻R上消耗的最大功率为P1 = I12R = 187.5 W。
,电路中的总电流最大,其最大值为I1 = E/R总= 10/0.4 A = 25 A,则电阻R上消耗的最大功率为P1 = I12R = 187.5 W。
设金属棒转到某位置时,QP间电阻为Rx,另一部分电阻为Ry,圆环接入电路的电阻为R圆环 =![]() 。当Rx = Ry = R1/2 = 0.2
。当Rx = Ry = R1/2 = 0.2![]() 时,圆环接入电路的电阻最大,其最大值为0.1
时,圆环接入电路的电阻最大,其最大值为0.1![]() ,此时通过负载电阻的电流最小,其最小值为I2 = E/R总= 10/(0.1 + 0.1 + 0.3) A = 20 A,则电阻R上消耗的最小功率为P2 = I22R = 120 W。
,此时通过负载电阻的电流最小,其最小值为I2 = E/R总= 10/(0.1 + 0.1 + 0.3) A = 20 A,则电阻R上消耗的最小功率为P2 = I22R = 120 W。


