题目内容
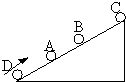 物块以v0=4m/s的速度滑上光滑的斜面,作匀减速直线运动.途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5s物块滑到斜面顶点C处速度变为零,已知 A、B相距0.75m,求斜面的长度?
物块以v0=4m/s的速度滑上光滑的斜面,作匀减速直线运动.途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5s物块滑到斜面顶点C处速度变为零,已知 A、B相距0.75m,求斜面的长度?分析:物体从A到B,根据速度位移公式有vB2-vA2=2asAB,从B到C,根据速度时间公式有0=vB+at0,结合A、B的速度关系,联立可求出物体的加速度B点的速度.知道了加速度和初速度,对DC段运用速度位移公式求出斜面的长度.
解答:解:物块作匀减速直线运动.设A点速度为vA、B点速度vB,加速度为a,斜面长为S.
A到B:vB2-vA2=2asAB …(1)
vA=2vB …(2)
B到C:0=vB+at0 …..(3)
解(1)(2)(3)得:vB=1m/s a=-2m/s2
D到C:0-v02=2aS …(4)
代入数据解得斜面的长度S=4m.
答:斜面的长度为4m.
A到B:vB2-vA2=2asAB …(1)
vA=2vB …(2)
B到C:0=vB+at0 …..(3)
解(1)(2)(3)得:vB=1m/s a=-2m/s2
D到C:0-v02=2aS …(4)
代入数据解得斜面的长度S=4m.
答:斜面的长度为4m.
点评:解决本题的关键掌握匀变速直线运动的速度位移公式v2-v02=2ax以及速度时间公式v=v0+at,并能灵活运用.

练习册系列答案
相关题目
 物块以v0=4m/s的速度滑上光滑的斜面D点,途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5秒物块滑到斜面顶点C速度变为零,A、B相距0.75米,求斜面的长度及物体由D运动到C的时间?
物块以v0=4m/s的速度滑上光滑的斜面D点,途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5秒物块滑到斜面顶点C速度变为零,A、B相距0.75米,求斜面的长度及物体由D运动到C的时间?