题目内容
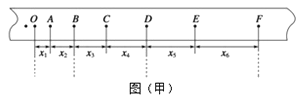
【题目】某同学利用电火花计时器研究做匀加速直线运动小车的运动情况，如图（甲）所示为该同学实验时打出的一条纸带中的部分计数点（后面计数点未画出），相邻计数点间有4个点迹未画出．所使用的交流电的频率为50 Hz．
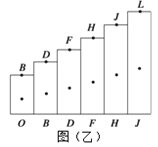
⑴为研究小车的运动，此同学用剪刀沿虚线方向把纸带上OB、BD、DF……等各段纸带剪下，将剪下的纸带一端对齐，按顺序贴好，如图（乙）所示．若各段纸带上方的左上角、中点或各段纸带的中点连接后为一条直线，则可以判断此小车_________（选填：“是”或“不是”）做匀变速直线运动．
⑵在图中x1＝7.05 cm、x2＝7.68 cm、x3＝8.31 cm、x4＝8.94 cm、x5＝9.57 cm、x6＝10.20 cm，则打下点迹A时，小车运动的速度大小是_________m/s，小车运动的加速度大小是_________m/s2．（本小题计算结果保留两位有效数字）
⑶如果当时电网中交流电的频率是f＝49 Hz而电压不变，而做实验的同学并不知道，由此引起的系统误差将使加速度的测量值___________实际值．（填“大于”，“等于”或“小于”）
⑷如果当时电网中交流电的电压变成210 V而频率不变，而做实验的同学并不知道，那么由此引起的系统误差使加速度的测量值与实际值相比__________．（填“偏大”、“偏小”或“不变”）
【答案】（1）是； （2）0.74； 0.63； （3）大于； （4）不变．
【解析】
（1）它们的长度分别等于x=v平均t，因为剪断的纸带所用的时间都是t=0.1s，即时间t相等，所以纸带的长度之比等于此段纸带的平均速度之比；而此段纸带的平均速度等于这段纸带中间时刻的速度，最后得出结论纸带的长度之比等于此段纸带的平均速度之比，还等于各段纸带中间时刻的速度之比，即纸带的高度之比等于中间时刻速度之比，因此图乙中的B、D、F、H、J、L，各点连起来恰好为一直线，说明每相邻两个纸带相差的长度相等，即△x=aT2，所以说明小车做匀变速直线运动；
（2）匀变速直线运动中时间中点的瞬时速度等于该过程中的平均速度，由此可得：
vA=
=
m/s=0.74m/s；
根据匀变速直线运动的推论△x=aT2，有：
x6-x3=3a1T2 ①
x5-x2=3a2T2 ②
x4-x1=3a3T2 ③
a=
=④
联立①②③④解得：a=
=0.63m/s2；
（3）若交变电流的频率是f=49Hz，则打点周期T大于0.02s，即使用公式a=
计算时所用T值偏小，则a偏大；
（4）打点计时器的打点周期与交流电的周期有关，与电压无关，故当电网中交流电的电压变成210V而频率不变，由此引起的系统误差使加速度的测量值与实际值相比不变
故答案为：（1）是；（2）0.74；0.63；（3）大于；（4）不变．
