题目内容
8. 如图所示,匀强磁场的磁感应强度为B,宽度为d,边界为CD和EF.一电子从CD边界外侧以速率v0垂直射入匀强磁场,入射方向与CD边界间夹角为θ.已知电子的质量为m,电荷量为e,为使电子能从磁场的另一侧EF射出,求电子的速率v0至少多大?若θ角可取任意值,v0的最小值是多少?
如图所示,匀强磁场的磁感应强度为B,宽度为d,边界为CD和EF.一电子从CD边界外侧以速率v0垂直射入匀强磁场,入射方向与CD边界间夹角为θ.已知电子的质量为m,电荷量为e,为使电子能从磁场的另一侧EF射出,求电子的速率v0至少多大?若θ角可取任意值,v0的最小值是多少?
分析 电子在磁场中做匀速圆周运动,当其轨迹恰好与EF边相切时,轨迹半径最小,对应的速度最小.由几何知识求出,再牛顿定律求出速度的范围.运用数学知识,由θ的取值来确定速度的最小,从而求出半径的最小值.
解答  解:当入射速率v0很小时,电子会在磁场中转动一段圆弧后又从CD一侧射出,
解:当入射速率v0很小时,电子会在磁场中转动一段圆弧后又从CD一侧射出,
速率越大,轨道半径越大,当轨道与边界EF相切时,电子恰好不能从EF射出,如图所示:
电子恰好射出时,由几何知识可得:
r+rcosθ=d ①
电子做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:ev0B=m$\frac{{v}_{0}^{2}}{r}$,
解得:r=$\frac{m{v}_{0}}{eB}$ ②
由①②得:v0=$\frac{eBd}{m(1+cosθ)}$ ③
故电子要射出磁场,速率至少应为:$\frac{eBd}{m(1+cosθ)}$.
由③式可知,θ=0°时,v0=$\frac{Bed}{2m}$最小,
由②式知此时半径最小,rmin=$\frac{d}{2}$,
答:为使电子能从磁场的另一侧EF射出,求电子的速率v0至少为$\frac{eBd}{m(1+cosθ)}$,θ角可取任意值,v0的最小值是:$\frac{Bed}{2m}$.
点评 本题考查圆周运动的边界问题的求解方法.当入射速率v0很小时,电子会在磁场中转动一段圆弧后又从CD一侧射出,速率越大,轨道半径越大,当轨道与边界EF相切时,电子恰好不能从EF射出.

练习册系列答案
相关题目
18.“连续物”是指和天体紧紧连接在一起的物体,“小卫星群”是指环绕天体运动的许多小星体的总称.据观测,在土星的外层有一个环,为了判定此环是土星的连续物还是土星的小卫星群,可测出环中各层的线速度v和该层到土星中心的距离R,进而得出v和R的关系,下列说法中正确的是( )
| A. | 若v和R成正比,则此环是连续物 | B. | 若v和R成正比,则此环是小卫星群 | ||
| C. | 若v2和R成反比,则此环是小卫星群 | D. | 若v2和R成反比,则此环是连续物 |
16.如图 所示为两个带等量点电荷周围的电场线分布(电场线方向未标出)( )


| A. | P、Q 是两个等量正电荷 | B. | P、Q 是两个等量负电荷 | ||
| C. | P、Q 是两个等量异种电荷 | D. | P、Q 产生的是匀强电场 |
20. 质量和电量都相等的带电粒子M和N,以不同的速度率经小孔S垂直进入均强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )
质量和电量都相等的带电粒子M和N,以不同的速度率经小孔S垂直进入均强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )
 质量和电量都相等的带电粒子M和N,以不同的速度率经小孔S垂直进入均强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )
质量和电量都相等的带电粒子M和N,以不同的速度率经小孔S垂直进入均强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )| A. | N的速度率大于M的速率 | B. | M、N的运行时间相同 | ||
| C. | 洛伦磁力对M、N做正功 | D. | M带正电,N带负电 |
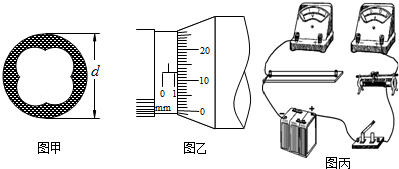
 如图电路中的电路元件A是电感器;C是电容器(填“电阻”、“电容器”、“电感器”或“电池”)
如图电路中的电路元件A是电感器;C是电容器(填“电阻”、“电容器”、“电感器”或“电池”)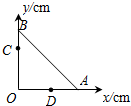 如图所示,等腰直角三棱镜ABO的两腰长都是16cm.为了测定它的折射率,棱镜放在直角坐标系中,使两腰与ox、oy轴重合.从OB边的C点注视A棱,发现A棱的视位置在OA边上的D点,在C、D两点插上大头针,看出C点的坐标位置(0、12),D点的坐标位置(9、0).由此计算出该棱镜的折射率为1.33.
如图所示,等腰直角三棱镜ABO的两腰长都是16cm.为了测定它的折射率,棱镜放在直角坐标系中,使两腰与ox、oy轴重合.从OB边的C点注视A棱,发现A棱的视位置在OA边上的D点,在C、D两点插上大头针,看出C点的坐标位置(0、12),D点的坐标位置(9、0).由此计算出该棱镜的折射率为1.33.