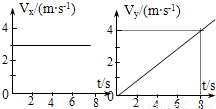题目内容
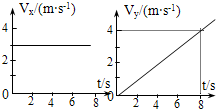 质量m=2㎏的物体在光滑的水平面上运动,其分速度Vx和Vy随时间变化的图线如图示,求:(1)物体受到的合力
质量m=2㎏的物体在光滑的水平面上运动,其分速度Vx和Vy随时间变化的图线如图示,求:(1)物体受到的合力(2)t=8s时物体的速度(大小、方向)
(3)t=4s时物体的位移(大小、方向)
分析:(1)运用运动的合成法研究物体的加速度,再由牛顿第二定律求解合力.由速度图象的斜率等于加速度,分别求出x轴和y轴方向物体的加速度,再求出合加速度,即可求解合力.
(2)由图读出t=8s时x轴和y轴方向的分速度,合成求出物体的速度.
(3)物体在x轴方向做匀速直线运动,y轴方向做匀加速运动,分别求出两个方向的分位移,再合成求解物体的位移.
(2)由图读出t=8s时x轴和y轴方向的分速度,合成求出物体的速度.
(3)物体在x轴方向做匀速直线运动,y轴方向做匀加速运动,分别求出两个方向的分位移,再合成求解物体的位移.
解答:解:(1)由图看出,物体在x轴方向做匀速直线运动,y轴方向做匀加速运动,则
a=ay=
=0.5m/s2,
由牛顿第二定律得,F合=ma=1N
(2)t=8s时,vx=3m/s,vy=4m/s,则v=
=5m/s
tanθ=
=
,θ=53°,即速度方向与x轴正方向成53°偏正y方向.
(3)t=4s时,x=vxt=12m,y=
at2=4m
故S=
=4
m/s,tanα=
=
,α=arctan
,即位移方向与速度方向与x轴正方向成arctan
偏正y方向.
答:(1)物体受到的合力是1N.
(2)t=8s时物体的速度大小是5m/s,方向为与x轴正方向成53°偏正y方向.
(3)t=4s时物体的位移大小是4
m/s,方向与速度方向与x轴正方向成arctan
偏正y方向.
a=ay=
| △vy |
| △t |
由牛顿第二定律得,F合=ma=1N
(2)t=8s时,vx=3m/s,vy=4m/s,则v=
|
tanθ=
| vy |
| vx |
| 4 |
| 3 |
(3)t=4s时,x=vxt=12m,y=
| 1 |
| 2 |
故S=
| x2+y2 |
| 10 |
| y |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
答:(1)物体受到的合力是1N.
(2)t=8s时物体的速度大小是5m/s,方向为与x轴正方向成53°偏正y方向.
(3)t=4s时物体的位移大小是4
| 10 |
| 1 |
| 3 |
点评:本题是运动的合成问题,包括加速度、速度、位移的合成,都按平行四边形定则进行合成.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
质量m=1kg的物体在光滑平面上运动,初速度大小为2m/s.在物体运动的直线上施以一个水平恒力,经过t=1s,速度大小变为4m/s,则这个力的大小可能是( )
| A、2 N | B、4 N | C、6 N | D、8 N |
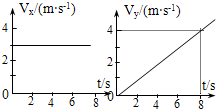 质量m=2㎏的物体在光滑的水平面上运动,其分速度Vx和Vy随时间变化的图线如图示,求:(1)物体受到的合力
质量m=2㎏的物体在光滑的水平面上运动,其分速度Vx和Vy随时间变化的图线如图示,求:(1)物体受到的合力