题目内容
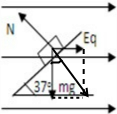
 如图,光滑绝缘斜面的倾角为37°,一带有正电荷的小物体质量为m,带电量为q置于斜面上,当沿水平向右加一个如图的匀强电场时,木块恰好静止在斜面上.求(1)原来电场强度;(2)从某时开始,电场强度减小为原来的
如图,光滑绝缘斜面的倾角为37°,一带有正电荷的小物体质量为m,带电量为q置于斜面上,当沿水平向右加一个如图的匀强电场时,木块恰好静止在斜面上.求(1)原来电场强度;(2)从某时开始,电场强度减小为原来的| 1 | 2 |
分析:(1)当带正电荷的物体在电场中静止于光滑绝缘斜面顶端,因此对其受力分析,利用力的处理来确定电场力的大小,从而算出电场强度大小.
(2)当改变电场强度后,由动能定理列方程计算沿斜面下滑距离为L时物体的动能.
(2)当改变电场强度后,由动能定理列方程计算沿斜面下滑距离为L时物体的动能.
解答:解:(1)受力分析,如图所示:物块受3个力而平衡,运用合成法,
由几何知识有:
=N---①
=N---②
则:
=tan37°=
得:E=
(2)当E减小为一半时,由动能定理:
Ek=F合l=(mgsin37°-
Eqcos37°)l=0.3mgl
答:(1)原来电场强度为
;
(2)沿斜面下滑距离为L时物体的动能0.3mgl.

由几何知识有:
| mg |
| cos37° |
| qE |
| sin37° |
| ② |
| ① |
| Eq |
| mg |
| 3 |
| 4 |
得:E=
| 3mg |
| 4q |
(2)当E减小为一半时,由动能定理:
Ek=F合l=(mgsin37°-
| 1 |
| 2 |
答:(1)原来电场强度为
| 3mg |
| 4q |
(2)沿斜面下滑距离为L时物体的动能0.3mgl.
点评:在物体下落过程中用动能定理,要注意电场力做功与沿电场力的位移有关,就像重力做功与高度相关一样.

练习册系列答案
相关题目
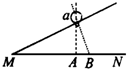
 有一光滑绝缘斜面体,如图所示,在斜面体上的a点与B点连线正好与斜面垂直,a点与A点相连正好与MN连线垂直.现把一带正电小球1放在光滑绝缘斜面的a点上,欲使小球1能静止该点位置,需在MN上放另一带电小球2,则小球2可能是( )
有一光滑绝缘斜面体,如图所示,在斜面体上的a点与B点连线正好与斜面垂直,a点与A点相连正好与MN连线垂直.现把一带正电小球1放在光滑绝缘斜面的a点上,欲使小球1能静止该点位置,需在MN上放另一带电小球2,则小球2可能是( )