��Ŀ����
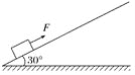
����Ŀ����ͼ����ʾ,һ������Ϊ0.6 kg ��С����ijһ���ٶȴ�P��ˮƽ�׳�,ǡ�ôӹ⻬Բ��ABC��A������߷������Բ��(���ƿ�������,����Բ��ʱ��е����ʧ)����֪Բ���İ뾶R=0.3 m,��=60��,С��A��ʱ���ٶ�vA=4 m/s��gȡ10 m/s2,��:
(1)С����ƽ���˶��ij��ٶ�v0��
(2)P����A��ĸ߶Ȳ�h��
(3)С��Բ����ߵ�Cʱ�Թ����ѹ��

���𰸡���1��2m/s����2��0.6m����3��8N��������ֱ���ϡ�
�����������������С��ǡ�ôӹ⻬Բ��ABC��A������߷������Բ���������ٶȵķֽ����������ٶ�v0�� P��A�Ĺ����ɶ��ܶ�����P����A��ĸ߶Ȳѡ���A��C���˶����̣����ö��ܶ������C���ٶȣ��ٸ�����������ʽ���С������ߵ�Cʱ�Թ����ѹ����
(1)�ٶȷֽ���ͼ��ʾ
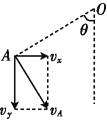
��ƽ���˶����ɵ�
v0=vx=vAcos��=2m/s
(2)С����P��A�Ĺ����ɶ��ܶ�����
![]()
��h=0.6m
(3)С���A�㵽C��Ĺ�����,�ɶ��ܶ�����
![]()
��![]()
С����C��ʱ��ţ�ٵڶ����ɵ�![]()
��![]()
��ţ�ٵ������ɵ�
FNC'=FNC=8N��������ֱ���ϡ�

��ϰ��ϵ�д�
 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
�����Ŀ