题目内容
6. 在光滑绝缘水平面上,一轻绳拉着一个带电小球绕竖直方向的轴O在匀强磁场中做逆时针方向的水平匀速圆周运动,磁场方向竖直向下,其俯视图如图所示.若小球运动到A点时,绳子突然断开,关于小球在绳断开后可能的运动情况,以下说法正确的是( )
在光滑绝缘水平面上,一轻绳拉着一个带电小球绕竖直方向的轴O在匀强磁场中做逆时针方向的水平匀速圆周运动,磁场方向竖直向下,其俯视图如图所示.若小球运动到A点时,绳子突然断开,关于小球在绳断开后可能的运动情况,以下说法正确的是( )| A. | 小球仍做逆时针匀速圆周运动,半径增大 | |
| B. | 小球仍做逆时针匀速圆周运动,但半径减小 | |
| C. | 小球做顺时针匀速圆周运动,半径不变 | |
| D. | 小球做顺时针匀速圆周运动,半径减小 |
分析 运动的带点粒子在磁场中受力洛伦兹力的作用,分小球带正电和负电两种情况进行讨论,用左手定则判断洛伦兹力的方向,根据向心力公式分析绳子所受的力,绳子断开后,绳子的拉力为零,小球仅受洛伦兹力,根据受力情况判断小球的运动情况即可.
解答 解:A、若小球带正电,则小球所受的洛伦兹力指向圆心,开始时,拉力可能为零,绳断后,仍然洛伦兹力提供向心力,逆时针做圆周运动,半径不变.
若开始靠洛伦兹力和拉力的合力提供向心力,拉力减小为零,小球靠洛伦兹力提供向心力,速度的大小不变,半径变大,故B错误,A正确.
C、如果小球带负电,则小球所受的洛伦兹力方向背离圆心,当洛伦兹力的大小等于小球原来所受合力大小时,绳子断后,小球做顺时针的匀速圆周运动,半径不变,也可能洛伦兹力小于之前合力的大小,则半径减小.故C、D正确.
故选:ACD
点评 该题考查带电粒子在磁场中的运动,解题的关键是能正确分析向心力的来源,结合受力分析判断洛伦兹力的方向,以及洛伦兹力的大小与初状态的合力的大小之间的关系,难度适中.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
11.如图所示,开关S合上瞬间,线圈B中( )


| A. | 无感应电流产生 | B. | 产生的感应电流方向为b→ →a →a | ||
| C. | 产生的感应电流方向为a→ →b →b | D. | 无法确定感应电流的方向 |
17. 如图所示,质量为M′的光滑斜面倾角为30°,质量分别为M、m的两个物体通过细绳及弹簧连接于光滑轻滑轮两侧,斜面底端有一与斜面垂直的挡板.开始时用手按住物体M,此时M距离挡板的距离为s,滑轮两边的细绳恰好伸直,且弹簧处于原长状态.已知M=2m,空气阻力不计.松开手后,斜面体始终保持静止,则在M下滑过程中下列说法中正确的是( )
如图所示,质量为M′的光滑斜面倾角为30°,质量分别为M、m的两个物体通过细绳及弹簧连接于光滑轻滑轮两侧,斜面底端有一与斜面垂直的挡板.开始时用手按住物体M,此时M距离挡板的距离为s,滑轮两边的细绳恰好伸直,且弹簧处于原长状态.已知M=2m,空气阻力不计.松开手后,斜面体始终保持静止,则在M下滑过程中下列说法中正确的是( )
 如图所示,质量为M′的光滑斜面倾角为30°,质量分别为M、m的两个物体通过细绳及弹簧连接于光滑轻滑轮两侧,斜面底端有一与斜面垂直的挡板.开始时用手按住物体M,此时M距离挡板的距离为s,滑轮两边的细绳恰好伸直,且弹簧处于原长状态.已知M=2m,空气阻力不计.松开手后,斜面体始终保持静止,则在M下滑过程中下列说法中正确的是( )
如图所示,质量为M′的光滑斜面倾角为30°,质量分别为M、m的两个物体通过细绳及弹簧连接于光滑轻滑轮两侧,斜面底端有一与斜面垂直的挡板.开始时用手按住物体M,此时M距离挡板的距离为s,滑轮两边的细绳恰好伸直,且弹簧处于原长状态.已知M=2m,空气阻力不计.松开手后,斜面体始终保持静止,则在M下滑过程中下列说法中正确的是( )| A. | M和m组成的系统机械能守恒 | |
| B. | 当M的速度最大时(未碰到板),m与地面间的作用力为零 | |
| C. | 当M的速度最大时(未碰到板),水平面对斜面的支持力为(M′+M+m)g | |
| D. | 当m离开地面后M做匀速运动 |
14.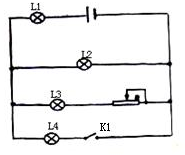 在如图所示的电路图中,开始时电键K1断开,L1至L4为电路中的四盏小灯泡,现在将L3所在电路的滑动变阻器的滑头向左移动则以下关于灯的亮暗变化正确的是( )
在如图所示的电路图中,开始时电键K1断开,L1至L4为电路中的四盏小灯泡,现在将L3所在电路的滑动变阻器的滑头向左移动则以下关于灯的亮暗变化正确的是( )
 在如图所示的电路图中,开始时电键K1断开,L1至L4为电路中的四盏小灯泡,现在将L3所在电路的滑动变阻器的滑头向左移动则以下关于灯的亮暗变化正确的是( )
在如图所示的电路图中,开始时电键K1断开,L1至L4为电路中的四盏小灯泡,现在将L3所在电路的滑动变阻器的滑头向左移动则以下关于灯的亮暗变化正确的是( )| A. | 灯L1变亮 | |
| B. | 灯L2变亮 | |
| C. | 灯L3变亮 | |
| D. | 若滑动变阻器滑头位置不变,现将电键K1闭合则灯L2变暗 |
1.下列实例中,不计空气阻力,机械能守恒的有( )
| A. | 做平抛运动的物体 | B. | 匀速上升的物体 | ||
| C. | 在竖直面内做匀速圆周运动的小球 | D. | 从高处沿粗糙曲面下滑的物体 |
15.一根轻质弹簧一端固定,用大小为F1的力压弹簧的另一端,平衡时长度为l1:改用大小为F2的力拉弹簧,平衡时长度为l2,弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为( )
| A. | $\frac{{F}_{2}+{F}_{1}}{{{l}_{2}-l}_{1}}$ | B. | $\frac{{F}_{2}+{F}_{1}}{{l}_{2}+{l}_{1}}$ | C. | $\frac{{F}_{2}+{F}_{1}}{{l}_{1}-{l}_{2}}$ | D. | $\frac{{F}_{2}-{F}_{1}}{{l}_{2}+{l}_{1}}$ |
16.关于做自由落体运动的小球,在落地之前的下列说法正确的是( )
| A. | 前2秒内和前4秒内下落的高度比为1:4 | |
| B. | 第5秒内和第7秒内下落的高度比为5:7 | |
| C. | 第1秒内和第2秒内的平均速度之比为1:3 | |
| D. | 下落第1米和下落第2米所用的时间之比为1:2 |
