Question

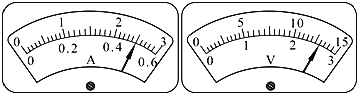
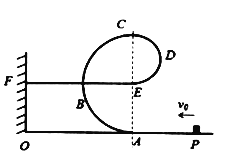
【题目】学校科技小组设计了“e”字型轨道竖直放置在水平面上，该轨道由两个光滑半圆形轨道ABC、CDE和粗糙的水平直轨道EF组成，末端与竖直的弹性挡板OF连接，轨道CDE半径r=0.1m，轨道ABC半径为2r，A端与地面相切。现将质量m=0.2kg小滑块从水平地面P点以速度v0=2m/s沿轨道上滑，运动到F点与挡板发生完全弹性相碰。已知直线轨道EF长为L=0.5m，小滑块与轨道EF的动摩擦因数μ=0.5，其余阻力均不计，小滑块可视为质点。求：

(1)小滑块在ABC圆轨道运动时对轨道C点的压力；

(2)小滑块最终停止的位置离F点的距离；

(3)若改变小滑块的初速度，使小滑块能停在EF轨道上，且运动过程中不脱离轨道，则小滑块的初速度满足什么条件。

Answer 1

【答案】(1)2N，竖直向上；(2)0.3m；(3)

【解析】

(1)小球从P到C的过程中，根据动能定理可得

在C点对小球根据牛顿第二定律

解得

根据牛顿第三定律可知小滑块对轨道的压力为2N，方向竖直向上。

(2)从P点到EF轨道停止过程中，根据动能定理

解得

所以小球最终停在离F点0.3m处。

(3)小球刚好经过最高点C，则

小球从P到C的过程中，根据动能定理可得

解得

当小球第一次从挡板弹回时，到达小圆的圆心等高处时速度为零，小球从P到D的过程中，根据动能定理可得

解得

所以小球的初速度范围为