题目内容
如图，细绳一端系着质量M=0.6kg的物体，静止在水平面，另一端通过光滑小孔吊着质量m=0.3kg的物体，M的中点与圆孔距离为0.2m，并知M和水平面的最大静摩擦力因数为μ=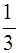
，现使此平面绕中心轴线转动，问角速度w在什么范围m会处于静止状态？(g取10m/s2)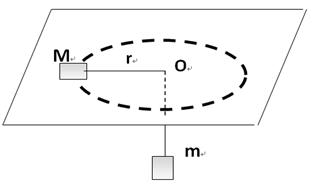
2.9 rad/s≤w ≤ 6.5 rad/s。
解析试题分析：设物体M和水平面保持相对静止。
当w具有最小值时，M有向圆心运动趋势，故水平面对M的摩擦力方向和指向圆心方向相反，且等于最大静摩擦力
隔离M有：T－μMg =Mw12r
w1 =2.9(rad/s)
当w具有最大值时，M有离开圆心趋势，水平面对M摩擦力方向指向圆心.
隔离M有：T＋μMg =Mw22r
w2=6.5(rad/s)
故w范围是：2.9 rad/s≤w ≤ 6.5 rad/s。
考点：此题考查圆周运动及牛顿定律。
练习册系列答案
相关题目
倍，试求：
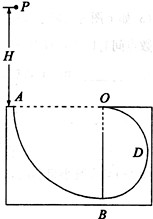
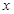.已知小球质量m，不计空气阻力，求：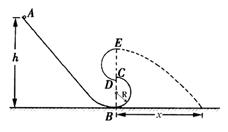
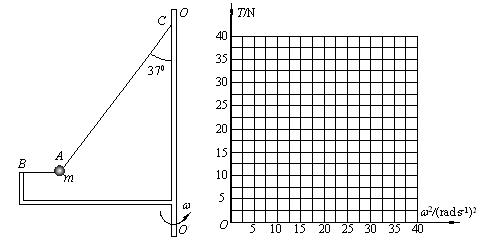
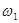时，细线AB上的张力为0而细线AC与竖直方向的夹角仍为37°，求角速度
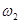时，细线AB刚好竖直，且张力为0，求此时角速度
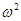变化的关系图像
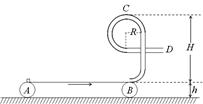
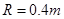的光滑半圆形细管与水平地面平滑相接，接触处静止一质量
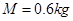的小球A，另一质量
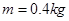的小球B静止于A右侧。现给小球B一水平向左的瞬时冲量，后经
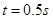B与 A相碰，碰后瞬间二者结为一体，恰好能沿细管运动至最高点。已知小球B与水平地面间的动摩擦因数
，重力加速度g取10m/s2。
