题目内容
【题目】2016年7月26日,九寨沟多处发生泥石流.假如一汽车停在小山坡底,突然司机发现山坡上距坡底240m处的泥石流以8m/s的初速度,0.4m/s2的加速度匀加速倾泻而下,假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动,若司机从发现情况到汽车启动需要4s时间,汽车启动后以恒定的加速度一直做匀加速直线运动.其过程简化为如图所示,求: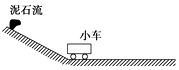
(1)泥石流到达坡底的时间和速度大小?
(2)试通过计算说明:汽车的加速度至少多大才能脱离危险?
【答案】
(1)解:设泥石流到达坡底的时间为t1,速度为v1,由题意有:v0=8m/s,0.4m/s2
![]()
v1=v0+a1t1
代入数据得:t1=20s,v1=16m/s
答:泥石流到达坡底的时间为20s,速度大小为16m/s
(2)解:汽车速度加速到等于v1且两者在水平地面的位移刚好相等就安全了,故依题意有:
v汽=a′t=v1…①
![]() …②
…②
泥石流在水平路面上的位移为:
s石=v1(t+4﹣t1)=s汽…③
由①②③代入数据可解得:a′=0.5m/s2
答:汽车的加速度至少为0.5m/s2才能脱离危险
【解析】(1)根据匀变速直线运动的位移时间关系和速度时间关系求得泥石流到达坡底的速度和时间;(2)根据汽车速度达到与泥石流速度相等的安全临界速度,再根据运动规律求解最小加速度.
【考点精析】根据题目的已知条件,利用匀变速直线运动的速度、位移、时间的关系和加速度的相关知识可以得到问题的答案,需要掌握速度公式:V=V0+at;位移公式:s=v0t+1/2at2;速度位移公式:vt2-v02=2as;以上各式均为矢量式,应用时应规定正方向,然后把矢量化为代数量求解,通常选初速度方向为正方向,凡是跟正方向一致的取“+”值,跟正方向相反的取“-”值;加速度与速度无关.只要速度在变化,无论速度大小,都有加速度;只要速度不变化(匀速),无论速度多大,加速度总是零;只要速度变化快,无论速度是大、是小或是零,物体加速度就大;方向与速度变化Δv的方向一致,但不一定与v的方向一致.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案