��Ŀ����
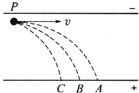
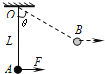
����Ŀ����ͼ��ʾ������Ϊm��С����Ϊ�ʵ㣩�ó�ΪL��ϸ��������O�㣬���ɾ�ֹ��Aλ�ã�����ˮƽ��F�����ؽ�С���A����Bλ�ö���ֹ��ϸ������ֱ����н�Ϊ��=60�㣬��ʱϸ�ߵ�����ΪF1��Ȼ�������С��Ӿ�ֹ���أ���A��ʱϸ�ߵ�����ΪF2���� ��
A��F1=F2=2mg
B����A��B������F����ΪF1L
C����B��A�Ĺ����У�С���ܵ��ĺ�������С����
D����B��A�Ĺ����У�С��������˲ʱ����һֱ����
���𰸡�A
��������
���������A����B�㣬����ƽ���У�F1sin30��=mg�����F1=2mg��
B��A�����ݶ��ܶ����ã�![]() ������ţ�ٵڶ����ɵã�
������ţ�ٵڶ����ɵã�![]() ��������ʽ���F2=2mg����A��ȷ��
��������ʽ���F2=2mg����A��ȷ��
B����A��B��С�����ƶ������ݶ��ܶ����ã�WF��mgL��1��cos60�㣩=0�����![]() ����B����
����B����
C����B��A�Ĺ����У�С����ٶȴ�С�ڱ仯������ĺ����ڱ仯����C����
D����B�㣬�����Ĺ���Ϊ�㣬����͵㣬�����ķ������ٶȷ���ֱ�������Ĺ���Ϊ�㣬��֪��B��A�Ĺ����У������Ĺ�����������С����D����
��ѡ��A��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ