题目内容
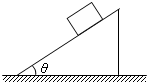 如图所示,质量为6kg的木块,放在倾角θ=37°的斜面上,木块与斜面间的动摩擦因数μ=0.25,木块距离斜面底端的距离为2m,若将木块由静止开始释放,(sin37°=0.6,cos37°=0.8),求:
如图所示,质量为6kg的木块,放在倾角θ=37°的斜面上,木块与斜面间的动摩擦因数μ=0.25,木块距离斜面底端的距离为2m,若将木块由静止开始释放,(sin37°=0.6,cos37°=0.8),求:(1)木块下滑到底端所需的时间;
(2)木块下滑到底端时的速度大小.
分析:根据牛顿第二定律求出木块下滑的加速度,结合时间公式求出木块下滑到底端所需的时间,根据速度时间公式求出木块下滑到底端时的速度大小.
解答:解:(1)根据牛顿第二定律得,mgsinθ-μmgcosθ=ma
解得a=gsinθ-μgcosθ=10×0.6-0.25×10×0.8m/s2=4m/s2.
由x=
at2得,运动的时间t=
=
s=1s.
(2)根据速度时间公式得,v=at=4×1m/s=4m/s.
答:(1)木块下滑到底端所需的时间为1s.
(2)木块下滑到底端时的速度大小为4m/s.
解得a=gsinθ-μgcosθ=10×0.6-0.25×10×0.8m/s2=4m/s2.
由x=
| 1 |
| 2 |
|
|
(2)根据速度时间公式得,v=at=4×1m/s=4m/s.
答:(1)木块下滑到底端所需的时间为1s.
(2)木块下滑到底端时的速度大小为4m/s.
点评:本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
相关题目
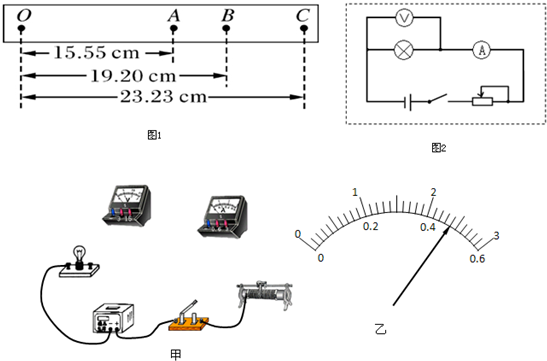
 (1)在研究碰撞中的动量守恒实验中,让质量为m1的小球从圆弧轨道上沿轨道向下运动,去碰原来静止在小支柱上的质量为m2的小球.
(1)在研究碰撞中的动量守恒实验中,让质量为m1的小球从圆弧轨道上沿轨道向下运动,去碰原来静止在小支柱上的质量为m2的小球.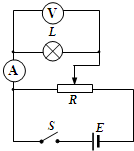 (2)(10分)有一个额定电压为2.8V,功率约为0.8W的小灯泡,现要用伏安法描绘这个灯泡的I-U图线,有下列器材供选用:
(2)(10分)有一个额定电压为2.8V,功率约为0.8W的小灯泡,现要用伏安法描绘这个灯泡的I-U图线,有下列器材供选用:

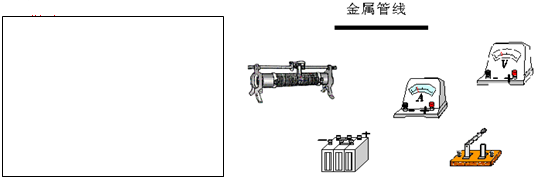
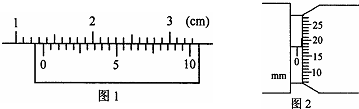 (1)有一游标卡尺,主尺的最小分度是1mm,游标上有20个小的等分刻度.用它测量一小球的直径,如图1所示的读数是
(1)有一游标卡尺,主尺的最小分度是1mm,游标上有20个小的等分刻度.用它测量一小球的直径,如图1所示的读数是