题目内容
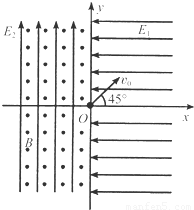
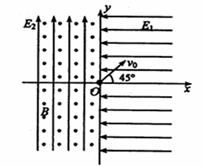
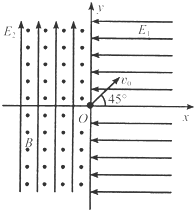 以竖直向上为y轴正方向的平面直角系xOy,如图所示.在第一、四象限内存在沿x轴负方向的匀强电场E1,在第二、三象限内存在着沿y轴正方向的匀强电场E2和垂直于xOy平面向外的匀强磁场.现有一质量为m、电荷量为q的带正电小球从坐标原点O以初速度v0沿与x轴正方向成45°角的方向射出.已知两电场的电场强度E1=E2=
以竖直向上为y轴正方向的平面直角系xOy,如图所示.在第一、四象限内存在沿x轴负方向的匀强电场E1,在第二、三象限内存在着沿y轴正方向的匀强电场E2和垂直于xOy平面向外的匀强磁场.现有一质量为m、电荷量为q的带正电小球从坐标原点O以初速度v0沿与x轴正方向成45°角的方向射出.已知两电场的电场强度E1=E2=| mg | q |
(1)求小球离开O点后第一次经过y轴所用的时间;
(2)求小球离开O点后第三次经过y轴的坐标;
(3)若小球从O点以某一初速度沿与x轴正方向成135°角的方向射出且能再次回到O点,则该初速度的大小为多少?
分析:(1)根据牛顿第二定律,可求出加速度大小与方向,再由运动学公式,即可求解;
(2)根据电场力与重力平衡,可知,粒子做匀速圆周运动,由牛顿第二定律,列式可得,半径关系.从而由粒子做平抛运动,运用运动学公式可得,每次经过y轴的坐标,从而即可求解;
(3)根据粒子做匀速圆周运动,由牛顿第二定律与几何关系可知,初速度的大小.
(2)根据电场力与重力平衡,可知,粒子做匀速圆周运动,由牛顿第二定律,列式可得,半径关系.从而由粒子做平抛运动,运用运动学公式可得,每次经过y轴的坐标,从而即可求解;
(3)根据粒子做匀速圆周运动,由牛顿第二定律与几何关系可知,初速度的大小.
解答:解: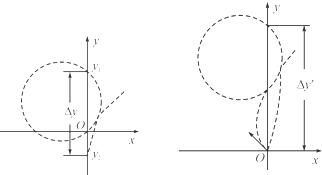 (1)设小球在第一象限中的加速度为a,
(1)设小球在第一象限中的加速度为a,
由牛顿第二定律得
=ma
得到a=
g,方向与v0的方向相反
在第一象限中小球先匀减速运动再反向匀加速运动,所以
t1=
=
(2)小球第一次经过y轴后,在第二、三象限内由qE=mg,电场力与重力平衡,故做匀速圆周运动.设轨迹半径为R.有
qv0B=m
得R=
小球第二次经过y轴的坐标
y1=
R=
t时间后第三次经过y轴,在第一、四象限内做类平抛运动,有
v0t′=
gt2
得t′=
小球第二次经过y轴与第三次经过y轴的距离为
△y=
v0t′=
小球第三次经过y轴的坐标y2=y1-△y=
-
(3)若小球沿与x轴正方向成135°射出时小球的运动轨迹如图所示,有△y′=2
R′
即
=2
得v=
答:(1)则小球离开O点后第一次经过y轴所用的时间
;
(2)则小球离开O点后第三次经过y轴的坐标
-
;
(3)若小球从O点以某一初速度沿与x轴正方向成135°角的方向射出且能再次回到O点,则该初速度的大小为
.
 (1)设小球在第一象限中的加速度为a,
(1)设小球在第一象限中的加速度为a,由牛顿第二定律得
| (mg)2+(qE)2 |
得到a=
| 2 |
在第一象限中小球先匀减速运动再反向匀加速运动,所以
t1=
| 2v0 |
| a |
| ||
| g |
(2)小球第一次经过y轴后,在第二、三象限内由qE=mg,电场力与重力平衡,故做匀速圆周运动.设轨迹半径为R.有
qv0B=m
| ||
| R |
得R=
| mv0 |
| qB |
小球第二次经过y轴的坐标
y1=
| 2 |
| ||
| qB |
t时间后第三次经过y轴,在第一、四象限内做类平抛运动,有
v0t′=
| 1 |
| 2 |
| 2 |
得t′=
| ||
| g |
小球第二次经过y轴与第三次经过y轴的距离为
△y=
| 2 |
| ||
| g |
小球第三次经过y轴的坐标y2=y1-△y=
| ||
| qB |
| ||
| g |
(3)若小球沿与x轴正方向成135°射出时小球的运动轨迹如图所示,有△y′=2
| 2 |
即
| 2v2 |
| g |
| 2 |
| mv |
| qB |
得v=
| ||
| qB |
答:(1)则小球离开O点后第一次经过y轴所用的时间
| ||
| g |
(2)则小球离开O点后第三次经过y轴的坐标
| ||
| qB |
| ||
| g |
(3)若小球从O点以某一初速度沿与x轴正方向成135°角的方向射出且能再次回到O点,则该初速度的大小为
| ||
| qB |
点评:考查粒子在电场力作用下做类平抛运动,在磁场力作用下做匀速圆周运动,掌握处理的方法与规律,理解牛顿第二定律与几何的关系的应用.本题画出正确的运动轨迹是解题的关键之处.

练习册系列答案
相关题目
 如图所示,在倾角为30°的光滑斜面上垂直纸面放置一根长为L,质量为m的通电直导体棒,棒内电流大小为I,方向垂直纸面向外.以水平向右为x轴正方向,竖直向上为y轴正方向建立直角坐标系.
如图所示,在倾角为30°的光滑斜面上垂直纸面放置一根长为L,质量为m的通电直导体棒,棒内电流大小为I,方向垂直纸面向外.以水平向右为x轴正方向,竖直向上为y轴正方向建立直角坐标系.
 ,磁场的磁感应强度为B.
,磁场的磁感应强度为B.