题目内容
铁路转弯处的弯道半径r是根据地形决定的,弯道处要求外轨比内轨高,其内外轨高度差h的设计不仅与r有关,还取决于火车在弯道上的行驶速率.下面表格中是铁路设计人员技术手册中弯道半径r及与之相对应的轨道高度差h的几组数据.
(1)根据表中数据,试导出h与r关系的表达式为 ,并求出当r=440m时,h的设计值应为 .
(2)铁路建成后,火车通过弯道时,为保证绝对安全,要求内外轨道均不向车轮施加侧面压力,火车通过弯道时的向心力大小为mgtgθ.其中m为火车的质量,θ为路轨与水平面间的夹角.已知我国铁路内外轨的间距设计值L=1.5m,结合表中数据,算出我国火车的转弯速率v= m/s.(计算时θ的正切值用正弦值来替代,保留一位小数.)
| 弯道半径r(m) | 660 | 330 | 220 | 165 | 132 | 110 |
| 内外轨高度差h(m) | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 |
(2)铁路建成后,火车通过弯道时,为保证绝对安全,要求内外轨道均不向车轮施加侧面压力,火车通过弯道时的向心力大小为mgtgθ.其中m为火车的质量,θ为路轨与水平面间的夹角.已知我国铁路内外轨的间距设计值L=1.5m,结合表中数据,算出我国火车的转弯速率v=
分析:要解答本题要求学生会看图表.能够很好的利用实验数据和数学图象,能够分析实验数据和认识数学图象,是物理中比较常见的题型.
解答:解:(1)由表中数据可见:弯道半径r越小,内外轨高度差h越大.
h与r成反比,即r?h=660×0.05=330×0.1=33
由 r?h=33,即h=
当r=440m时,h=
m=0.075m.
(2)转弯中,当内外轨对车轮均没有侧向压力时,火车的受力如图
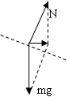
由牛顿第二定律得mgtanα=m
因为α很小,有tanα=sina=
则v=
,代入数据解得v=14.8m/s.
故答案为:(1)h=
,0.075.(2)14.8.
h与r成反比,即r?h=660×0.05=330×0.1=33
由 r?h=33,即h=
| 33 |
| r |
当r=440m时,h=
| 33 |
| 440 |
(2)转弯中,当内外轨对车轮均没有侧向压力时,火车的受力如图

由牛顿第二定律得mgtanα=m
| v2 |
| r |
因为α很小,有tanα=sina=
| h |
| L |
则v=
|
故答案为:(1)h=
| 33 |
| r |
点评:此类题要求学生根据题给信息,通过分析、探究出相关量之间的关系,由于此类题突出体现了过程与方法,能较好地考查学生的科学探究能力和创新思维能力.

练习册系列答案
相关题目