题目内容
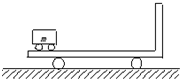 (2005?西城区模拟)如图所示,质量为M=20kg的平板车静止在光滑的水平面上;车上最左端停放着质量为m=5kg的电动车,电动车与平板车上的挡板相距L=5m.电动车由静止开始向右做匀加速运动,经时间t=2s电动车与挡板相碰,问:
(2005?西城区模拟)如图所示,质量为M=20kg的平板车静止在光滑的水平面上;车上最左端停放着质量为m=5kg的电动车,电动车与平板车上的挡板相距L=5m.电动车由静止开始向右做匀加速运动,经时间t=2s电动车与挡板相碰,问:(1)碰撞前瞬间两车的速度大小各为多少??
(2)若碰撞过程中无机械能损失,且碰后电动机关闭并刹车,使电动车只能在平板车上滑动,要使电动车不脱离平板车,它们之间的动摩擦因数至少多大?
分析:由题意知电动车和长木板车均做初速度为0的匀加速直线运动,已知运动时间和运动总位移,根据初速度为0的匀加速直线运动的平均速度和动量守恒定律可以解得与挡板相碰时两车的速度;碰撞后电动车刹车,由于在碰撞前后动量和机械能均守恒,故可以知道碰撞后两车只是改变速度方向不改变速度的大小,根据能量守恒和动量守恒知,两车相对静止时均对地面静止,根据电动车克服摩擦力做的功等于系统机械能的减小量可以求出长木板车与电动车间的最小动摩擦因数μ.
解答:解:(1)如图,电动车向右运动的过程中长板车将向左运动,在运动过程中满足动量守恒

由图可知,令电动车相对地面产生的位移大小为x,则长木板车的位移大小为(L-x),负号表示长木板车的位移方向与电动车位移方向相反,令与挡板相碰前电动车的速度为vm,长木板车的速度vM,则据动量守恒有:
mvm+MvM=0…①
又因为在碰撞前两车均做初速度为0的匀加速运动,所以有:
=
,电动车运动的时间t=
=
=2s…②
=
,长木板车运动的时间t=
=
=2s…③
由①②③式可解得:
vm=4m/s
vM=1m/s
(2)因为在碰撞过程中无机械能损失,又因为在碰撞中系统动量守恒可知碰撞前后,两车速度均反向,且不改变原速度的大小
vm′=4m/s,方向向左;
vM′=1m/s,方向向右.
∵MvM=mvm
∴系统总动量为0,即当系统稳定时两车均静.
因为克服摩擦力做的功应该等于系统损失的机械能,要使电动车不滑离长木板车,则长木板车的长度满足:
μmgL≥
mvm′2+
MvM′2
代入数据可解得:μ≥0.2
答:(1)碰撞前瞬间两车的速度大小分别为vm=4m/s,vM=1m/s?
(2)若碰撞过程中无机械能损失,且碰后电动机关闭并刹车,使电动车只能在平板车上滑动,要使电动车不脱离平板车,它们之间的动摩擦因数至少为0.2.

由图可知,令电动车相对地面产生的位移大小为x,则长木板车的位移大小为(L-x),负号表示长木板车的位移方向与电动车位移方向相反,令与挡板相碰前电动车的速度为vm,长木板车的速度vM,则据动量守恒有:
mvm+MvM=0…①
又因为在碰撞前两车均做初速度为0的匀加速运动,所以有:
. |
| vm |
| vm |
| 2 |
| x | ||
|
| 2x |
| vm |
. |
| vM |
| vM |
| 2 |
| L-x | ||
|
| 2(L-x) |
| vM |
由①②③式可解得:
vm=4m/s
vM=1m/s
(2)因为在碰撞过程中无机械能损失,又因为在碰撞中系统动量守恒可知碰撞前后,两车速度均反向,且不改变原速度的大小
vm′=4m/s,方向向左;
vM′=1m/s,方向向右.
∵MvM=mvm
∴系统总动量为0,即当系统稳定时两车均静.
因为克服摩擦力做的功应该等于系统损失的机械能,要使电动车不滑离长木板车,则长木板车的长度满足:
μmgL≥
| 1 |
| 2 |
| 1 |
| 2 |
代入数据可解得:μ≥0.2
答:(1)碰撞前瞬间两车的速度大小分别为vm=4m/s,vM=1m/s?
(2)若碰撞过程中无机械能损失,且碰后电动机关闭并刹车,使电动车只能在平板车上滑动,要使电动车不脱离平板车,它们之间的动摩擦因数至少为0.2.
点评:熟悉系统动量守恒条件,能根据运动特征求出初速度为0的匀加速直线运动的速度与时间以及位移的关系,是解决第一问的关键,在第二问中,能从能量守恒角度确定克服摩擦力做的功等于系统机械能的减少量.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
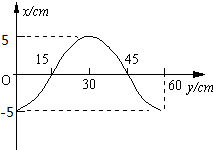 (2005?西城区模拟)如图所示为波源O振动1.5s时沿波的传播方向上部分质点振动的波形图,已知波源O在t=0时开始沿x轴负方向振动,t=1.5s时它正好第二次到达波谷,问:
(2005?西城区模拟)如图所示为波源O振动1.5s时沿波的传播方向上部分质点振动的波形图,已知波源O在t=0时开始沿x轴负方向振动,t=1.5s时它正好第二次到达波谷,问: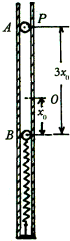 (2005?西城区模拟)质量为m的小球B用一根轻质弹簧连接.现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为x0,如图所示,小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动,并恰能回到0点(设两个小球直径相等,且远小于x0略小于直圆筒内径),已知弹簧的弹性势能为
(2005?西城区模拟)质量为m的小球B用一根轻质弹簧连接.现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为x0,如图所示,小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动,并恰能回到0点(设两个小球直径相等,且远小于x0略小于直圆筒内径),已知弹簧的弹性势能为