题目内容
【题目】横截面为直角三角形的两个相同斜面紧靠在一起,固定在水平面上,如图所示。它们的竖直边长都是底边长的一半。现有三个小球从左边斜面的顶点以不同的初速度向右平抛,最后落在斜面上,其落点分别是a、b、c 。下列判断正确的是
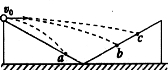
A.三小球比较,落在a点的小球飞行时间最短
B.三小球比较,落在c点的小球飞行过程速度变化最大
C.三小球比较,落在c点的小球飞行过程速度变化最快
D.无论小球抛出时初速度多大,落到斜面上的瞬时速度都不可能与斜面垂直
【答案】D
【解析】
试题分析:三个小球做平抛运动,从图中可知落在a点的小球下落的高度最大,根据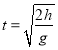 可得落在a点的小球运动时间最长,A错误;三个小球都做平抛运动,加速度都等于重力加速度,所以三个小球在飞行过程中速度变化率是一样的,根据公式
可得落在a点的小球运动时间最长,A错误;三个小球都做平抛运动,加速度都等于重力加速度,所以三个小球在飞行过程中速度变化率是一样的,根据公式![]() 可得落在a点的小球的速度变化量最大,故BC错误;首先落在a点的小球不可能与斜面垂直,b、c点,竖直速度是gt,水平速度是v,然后斜面的夹角是arctan0.5,要合速度垂直斜面,把两个速度合成后,需要
可得落在a点的小球的速度变化量最大,故BC错误;首先落在a点的小球不可能与斜面垂直,b、c点,竖直速度是gt,水平速度是v,然后斜面的夹角是arctan0.5,要合速度垂直斜面,把两个速度合成后,需要![]() ,即v=0.5gt,那么在经过t时间的时候,竖直位移为0.5gt2,水平位移为
,即v=0.5gt,那么在经过t时间的时候,竖直位移为0.5gt2,水平位移为![]() 即若要满足这个关系,需要水平位移和竖直位移都是一样的,显然在图中b、c是不可能完成的,因为在b、c上水平位移必定大于竖直位移,所以落到两个斜面上的瞬时速度都不可能与斜面垂直,故D正确.
即若要满足这个关系,需要水平位移和竖直位移都是一样的,显然在图中b、c是不可能完成的,因为在b、c上水平位移必定大于竖直位移,所以落到两个斜面上的瞬时速度都不可能与斜面垂直,故D正确.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目