题目内容
4.航天飞机水平降落在平直跑道上,其减速过程可简化为两个匀减速直线运动.航天飞机以水平速度v0着陆后立即打开减速阻力伞,加速度大小为a1,运动一段时间后减速为v;随后在无阻力伞情况下匀减速直至停下,已知两个匀减速滑行过程的总时间为t,求:(1)第二个减速阶段航天飞机运动的加速度大小
(2)航天飞机降落后滑行的总路程.
分析 (1)根据速度时间关系求解出第一段的时间,然后利用速度时间关系可求出第二段加速度;
(2)根据速度位移关系列式求解即可.
解答 解:(1)如图,A为飞机着陆点,AB、BC分别为两个匀减速运动过程,
C点停下.
A到B过程,依据v=v0+at有:
第一段匀减速运动的时间为:${t}_{1}=\frac{v-{v}_{0}}{-{a}_{1}}=\frac{{v}_{0}-v}{{a}_{1}}$
则B到C过程的时间为:${t}_{2}=t-{t}_{1}=t-\frac{{v}_{0}-v}{{a}_{1}}$
依据v=v0+at有:
B到C过程的加速度大小为:${a}_{2}=\frac{{v}_{c}-{v}_{b}}{{t}_{2}}=\frac{v}{t-\frac{{v}_{0}-v}{{a}_{1}}}=\frac{{a}_{1}v}{{a}_{1}t-{v}_{0}+v}$
(2)根据${v}^{2}-{{v}_{0}}^{2}=2x$得:
第一段匀减速的位移 ${x}_{1}=\frac{{v}^{2}-{{v}_{0}}^{2}}{-2{a}_{1}}=\frac{{{v}_{0}}^{2}-{v}^{2}}{2{a}_{1}}$
第二段匀减速的位移为:${x}_{2}=\frac{0-{v}^{2}}{-2{a}_{2}}=\frac{{v}^{2}}{2\frac{{a}_{1}v}{t-{v}_{0}+v}}=\frac{v({a}_{1}t-{v}_{0}+v)}{2{a}_{1}}$
所以航天飞机降落后滑行的总路程为:$x={x}_{1}+{x}_{2}=\frac{v{a}_{1}t-v{v}_{0}+{{v}_{0}}^{2}}{2{a}_{1}}$
答:(1)第二个减速阶段航天飞机运动的加速度大小为$\frac{{a}_{1}v}{{a}_{1}t-{v}_{0}+v}$;
(2)航天飞机降落后滑行的总路程为$\frac{vt{a}_{1}-v{v}_{0}+{{v}_{0}}^{2}}{2{a}_{1}}$.
点评 本题考查匀变速直线运动的速度时间关系和速度位移关系,属于基本题目,但要特别注意计算.

 特高级教师点拨系列答案
特高级教师点拨系列答案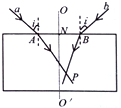 如图所示,直线OO′与上下表面平行的玻璃砖垂直且与其上表面交于N点.a,b两种单色光以相同的入射角i射到玻璃砖的上表面,入射点A、B到N点的距离相等,经折射后两束光相交于图中的P点.下列说法正确的是( )
如图所示,直线OO′与上下表面平行的玻璃砖垂直且与其上表面交于N点.a,b两种单色光以相同的入射角i射到玻璃砖的上表面,入射点A、B到N点的距离相等,经折射后两束光相交于图中的P点.下列说法正确的是( )| A. | a光在玻璃中的折射率比b光的大 | |
| B. | a光在玻璃中的传播速度比b光的小 | |
| C. | 对同一双缝干涉装置,a光的条纹间距比b光的小 | |
| D. | 增大i(i<90°),a.b光总能从玻璃砖的下表面射出 |
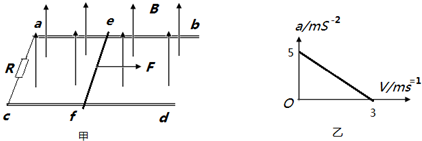
| A. | 一定做匀变速直线运动,加速度大小可能是5m/s2 | |
| B. | 可能做匀减速直线运动,加速度大小是2m/s2 | |
| C. | 一定做加速度不变的变速运动,加速度大小可能是15m/s2 | |
| D. | 可能做匀速圆周运动,向心加速度大小可能是5m/s2 |
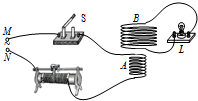 如图,多匝线圈A与电键、滑动变阻器相连后接入M、N间的交流电源,B线圈与小灯泡L相连.下列说法正确的是( )
如图,多匝线圈A与电键、滑动变阻器相连后接入M、N间的交流电源,B线圈与小灯泡L相连.下列说法正确的是( )| A. | L发光时,电路中发生了自感现象 | |
| B. | L发光时,A线圈的输入功率等于B线圈的输出功率 | |
| C. | 只有在闭合电键瞬间,L才能发光 | |
| D. | 若闭合电键后L不发光,将滑动变阻器滑片左移后,L可能会发光 |
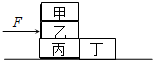 如图所示,用水平力F推乙物块,使甲、乙、丙、丁四个完全相同的物块一起沿水平地面以相同的速度匀速运动,各物块受到摩擦力的情况是( )
如图所示,用水平力F推乙物块,使甲、乙、丙、丁四个完全相同的物块一起沿水平地面以相同的速度匀速运动,各物块受到摩擦力的情况是( )| A. | 甲物块受到一个摩擦力的作用 | B. | 乙物块受到一个摩擦力的作用 | ||
| C. | 丙物块受到一个摩擦力的作用 | D. | 丁物块没有受到摩擦力的作用 |
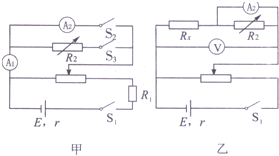 要用伏安法较准确地测量一约为100的定值电阻的阻值,除待测电阻外,提供的实验器材如下:
要用伏安法较准确地测量一约为100的定值电阻的阻值,除待测电阻外,提供的实验器材如下: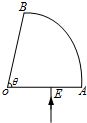 如图所示,AOB是截面为扇形的玻璃砖的横截面图,其顶角θ=76°.有一细束单色光在横截面内从OA边上的点E沿垂直OA的方向射入玻璃砖,光线直接到达AB面且刚好不从AB面射出.已知OE=$\frac{3}{5}$OA,cos53°=0.6,求玻璃砖的折射率n和光线第一次从OB射出时折射角的正弦值.
如图所示,AOB是截面为扇形的玻璃砖的横截面图,其顶角θ=76°.有一细束单色光在横截面内从OA边上的点E沿垂直OA的方向射入玻璃砖,光线直接到达AB面且刚好不从AB面射出.已知OE=$\frac{3}{5}$OA,cos53°=0.6,求玻璃砖的折射率n和光线第一次从OB射出时折射角的正弦值.