题目内容
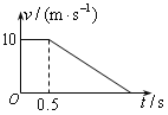
【题目】一宇宙空间探测器从某一星球的表面升空,假设探测器的质量恒为1500kg,发动机的推力为恒力,宇宙探测器升空到某一高度时,发动机突然关闭,如图是表示其速度随时间变化规律:

①求宇宙探测器在该行星表面所能到达的最大高度?
②假设行星表面没有空气,试计算发动机的推力。
③若该行星的半径为R,万有引力常量为G,则该行星的密度是多少?(用R、G表示)
【答案】①768m. ②18000N ③ρ=![]()
【解析】
①空间探测器上升的所能达到的最大高度应等于它在第一、第二运动阶段中通过的总位移值,所以有Hm=![]() =768m.
=768m.
②选取空间探测器为研究对象,空间探测器的发动机突然关闭后,它只受该行星的重力的作用,故它运动的加速度即为该行星表面处的重力加速度值,从v-t图线不难发现,8s末空间探测器关闭了发动机,所以v-t图线上的斜率即等于该行星表面处的重力加速度g=4m/s2。在0~8 s内,空间探测器受到竖直向上的推进力与竖直向下的重力的共同作用,则由牛顿第二定律得F-mg=ma又a=![]() =8m/s2
=8m/s2
故有F=(ma+mg)=18000N.
③根据![]() 且
且![]()
解得:ρ=![]() 得ρ=
得ρ=![]()

练习册系列答案
相关题目