题目内容
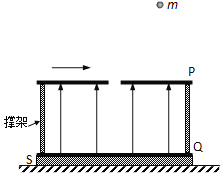
【题目】如图，绝缘平板S放在水平地面上，S与水平面间的动摩擦因数μ=0.4，两足够大的平行金属板P、Q通过绝缘撑架相连，Q板固定在平板S上，P、Q间存在竖直向上的匀强电场，整个装置总质量M=0.48kg，P、Q间距为d=lm，P板的中央有一小孔给装置某一初速度，装置向右运动。现有一质量m=0.04kg、电量q=+1×10-4C的小球，从离P板高h=1.25m处静止下落，恰好能进入孔内，小球进入电场时，装置的速度为
=5m/s。小球进入电场后，恰能运动到Q板且不与Q板接触，忽略平行金属板外部的电场对小球运动的影响。不计空气阻力，g取10m/s2。
(1)求匀强电场的场强大小E；
(2)求当小球第一次返回到P板时，装置的速度
；
(3)小球第一次与P板碰撞时间极短，碰后速度大小不变，方向反向，碰后电量变为q′ =-4×10-4C。求从小球进入电场到第二次到达Q板过程中，绝缘平板S与地面因为摩擦而产生的热量。(由于小球帶电量很小，碰撞过程对P、Q上的电荷分布的影响可以忽略，可认为碰撞前后两金属板间的电场保持不变)
【答案】（1）9×103N/C （2）1.2m/s （3）5.7096J
【解析】(1)小球下落到Q板时速度为零，从最高点到最低点过程，由动能定理得：
mg(h+d)Eqd=0,解得：E=9×103N/C；
(2)小球在电场中的加速度：a=（qEmg）/m=（1×104×9×1030.04×10）/0.04=12.5m/s2
小球在电场中运动的时间：t2=
，
小球进入电场后,装置的加速度：a′=μ(Mg+qE)/M=4.75m/s2
当小球第一次返回到P板时,装置的速度：v2=v1a′t2=54.75×0.8=1.2m/s；
(3)小球从进入电场到小球返回到P板过程中装置的位移： 
，
热量：Q1=μ(Mg+Eq)x1,解得：Q1=5.6544J，
小球与P板碰撞之后速度v0=5m/s，在之后的运动过程中：
小球的加速度：a′=（mg+q′E）/m=（0.04×10+4×104×9×103）/0.04=100m/s2
小球从P板运动至Q板的时间： 
,解得：t3=0.1s，
装置的加速度：a′2=μ(Mgq′E)/M=0.4×(0.48×104×104×9×103)/0.48=1m/s2
装置在这段时间内的位移： 
,热量：Q2=μ(MgEq′)x2，
解得：x2=0.115m,Q2=0.0552J,
产生的总热量：Q总=Q1+Q2=5.7096J；
