��Ŀ����
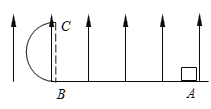
����Ŀ����ͼ��ʾ����ֱ���õİ�Բ�ξ�Ե����뾶ΪR���¶����Եˮƽ��ƽ�����ӣ�����װ�ô��ڷ�����ֱ���ϵ���ǿ�糡E�У�һ����Ϊm��������Ϊ![]() ����飨����Ϊ�ʵ㣩����ˮƽ���ϵ�A���Գ��ٶ�v0ˮƽ�����˶����ذ�Բ�ι��ǡ��ͨ����ߵ�C����ǿ��СΪE����
����飨����Ϊ�ʵ㣩����ˮƽ���ϵ�A���Գ��ٶ�v0ˮƽ�����˶����ذ�Բ�ι��ǡ��ͨ����ߵ�C����ǿ��СΪE����![]() ,����
,����
��1����龭����ߵ�C���ٶ�Ϊ���
��2���Լ���������˶������п˷�Ħ�������Ĺ���
��3��֤������뿪������ˮƽ���ˮƽ�����볡ǿ��СE�أ���Ϊһ������
���𰸡�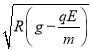
![]()
![]()
�������������������1������ǡ��ͨ����ߵ� C���������͵糡���ṩ����������ţ�ٵڶ����ɼ������C����ٶȣ���2����A��C�ɶ��ܶ�������������˷�Ħ�������Ĺ�����3�������뿪��Բ�ι��������ƽ���˶���������ƽ���˶��Ĺ��ɼ�����⡣
��1�����ǡ��ͨ��Բ����ߵ�C��Բ�������ʱ�������������ã�����ܵ��������͵糡���ṩ����������ţ�ٵڶ������У� ![]() ����ã�
����ã� 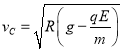
��2���������A�˶���C�Ĺ����У������˷�Ħ�������Ĺ�![]()
�ɶ��ܶ����У� ![]()
��ã� ![]()
��3������뿪��Բ�ι��������ƽ���˶�����ˮƽλ��ΪS��
ˮƽ�����У� ![]()
��ֱ�����У� ![]()
������ã� ![]()
��ˣ�����뿪������ˮƽ���ˮƽ�����볡ǿ��СE�أ���СΪ2R