Question

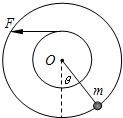（2006?上海）半径分别为r和2r的两个质量不计的圆盘，共轴固定连接在 一起，可以绕水平轴O无摩擦转动，大圆盘的边缘上固定有  一个质量为m的质点，小圆盘上绕有细绳．开始时圆盘静止，质点处在水平轴O的正下方位置．现以水平恒力F拉细绳，使两圆盘转动，若恒力 F=mg，两圆盘转过的角度θ=

π

6

时，质点m的速度最大．若圆盘转过的最大角度θ=π/3，则此时恒力F=

3mg

π

．

Answer 1

分析：当F的力矩大于mg的力矩时，质点m的速度增大，当F的力矩小于mg的力矩时，质点m的速度减小，则当两者力矩相等时，质点m的速度最大．根据力矩平衡条件列方程求解．再能量守恒定律求解F．

解答：解：当F的力矩等于mg的力矩时，质点m的速度最大．
    则有Fr=mg?2rsinθ
        又F=mg
     解得θ=

π

6

  根据能量守恒定律得
     F?

π

3

r=mg?2rcos

π

3

   解得F=

3mg

π

本题答案是：

π

6

，

3mg

π

点评：本题解题关键在于分析什么时候质点的速度最大，要根据力矩的作用使物体产生转动来分析．