Question

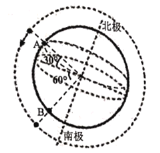
【题目】一个半径为R的绝缘圆柱面，有2N+1根长为L的直铜导线紧紧贴在其表面，通有向下的电流，大小均为I,通电导线有两种放置方法。方法1:如图甲(俯视图为丙),一根放置在AA'处，其余2N根均匀、对称的分布在圆柱的右半侧，与圆柱的轴平行;方法2:如图乙(俯视图为丁)，一根放置在AA'处，其余2N根均匀、对称的分布在圆柱的左半侧，与圆柱的轴平行。在这两种情况下，其余2N根在AA'处产生的磁场分别为B1、B2，放置在AA'处的导线受安培力分别为F1、F2。已知通有电流i的长直导线在距其r处产生的磁感应强度大小为 (其中km为一常数)。则

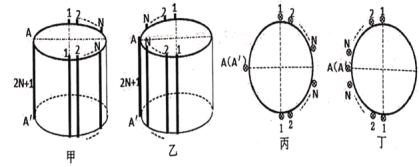
A.B1、B2方向不同B.B1、B2方向相同

C.D.

Answer 1

【答案】BC

【解析】

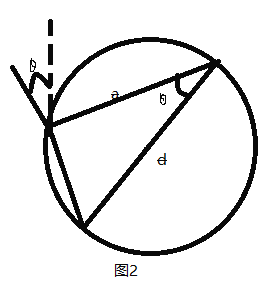
AB．以2N中在一根通电直导线为研究对象，在A点产生磁场是以此导线所在位置为圆心，两直导线连线为半径在圆上的切线，如图1所示，其水平向合磁感应强度为0，则总的磁感应强度为竖直向上，选图中的任一条求其沿竖直向上的分量：设图丙中的2离A点距离为a，d为圆直径。如图2，丙图中的任一根在A产生的磁场B的向上（丙图方位）分量为

即任一根在图中的任何位置在竖直向上的分量的值都是相同的，则在A处的总的磁感应强度为，故A错误，B正确；

CD．放置在AA′处的导线受安培力相等，有

故C正确，D错误。

故选BC。