题目内容
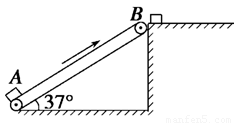
如图所示，传送带以4m/s的速度沿图示方向匀速运动。已知传送带的总长度为l=4m。现将一质量m=0.6kg的可看作质点的小木块放到传送带的左端，使它具有初速度v。已知木块与传送带间的动摩擦因数为μ=0.20，取g=10m/s2。求木块的初速度分别等于下面的数值时，木块在传送带上运动的整个过程中，摩擦力对木块的冲量。（取g=10m/s2）
①v=v1=2m/s。 ②v=v2=6m/s。
（1）1.2N·s，方向向右 （2）0.91N·s，方向向左
解析:
①由于木块的初速度v1<v0。因此木块相对于传送带向后运动，受到的摩擦力方向向前，大小为f=μmg，加速度大小a = f / m=μg= 2 m/s2。
木块速度达到与传送带速度相等所用时间 t1=（v0- v1）/ a=1.0 s，
位移大小 s1=（v02- v12）/2a = 3m。说明木块尚未到达传送带右端即与传送带速度相等，此后木块就与传送带以相同的速度匀速运动，二者间没有摩擦力了。
因此，摩擦力对木块的冲量大小为I= f·t =μmg·t=1.2N·s，方向向右。
②由于木块的初速度v2>v0。木块相对于传送带向前运动，受到的摩擦力方向向后，大小为f=μmg, 加速度大小a’= f / m=2m/s2。
如果木块的速度达到与传送带相等，位移大小为 s’=（v22- v02）/2a’ = 5m., 说明木块尚未达到与传送带速度相等，就已经滑出传送带。
它滑出传送带所需的时间t2可用公式l= v2t2-a’ t22/2计算，代入数值解得 t2=3±
，取符合题意的解t2=（3-）s=0.76s。（另一个解t2=-（3+）s>1s，不合题意，舍去。）
因此摩擦力对木块的冲量大小 I=μmg·t2=0.91N·s，方向向左。
在工厂的流水线上安装有传送带，用传送带传送工件，可大大提高工作效率．如图所示，传送带与水平面夹角为θ=30°，其上、下两端点A、B间的距离是3.84m．传送带在电动机的带动下，以4.0m/s顺时针匀速运转．现将质量为10kg的工件（可视为质点）轻放于传送带的A点，已知工件与传送带间的动摩擦因数为
如图所示，传送带的两个轮子半径均为r=0.2m，两个轮子最高点A、B在同一水平面 内，A、B间距离L=5m，半径R=0.4的固定、竖直光滑圆轨道与传送带相切于B点，C 点是圆轨道的最高点．质量m=0.1kg的小滑块与传送带之间的动摩擦因数μ=0.4．重力加速 度 g=10m/s2．求：
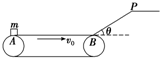如图所示，传送带以v0=5m/s的速度顺时针转动，水平部分AB=s=1.5m，一质量为m=0.4kg的小工件由A点轻轻放上传送带，工件与斜面间的动摩擦因数为μ1=
| ||
| 6 |
| A、工件从A到B先做匀加速运动再做匀速运动 |
| B、工件与传送带间的动摩擦因数为0.3 |
| C、工件运动到B点时摩擦力的功率为6W |
| D、工件从A运动到P的过程中因摩擦而产生的热量为4.2J |
