题目内容
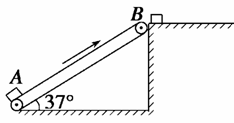
(19分)如图所示的传送带装置,长度为4 m,与水平方向之间的夹角为37°,传送带以0.8 m/s的速度匀速运行,从流水线上下来的工件每隔2 s有一个落到A点(可认为初速度为零),工件质量为1 kg.经传送带运送到与B等高处的平台上,再由工人运走.已知工件与传送带之间的动摩擦因数为μ=0.8,sin 37°=0.6,cos 37°=0.8,g=10 m/s2.求:
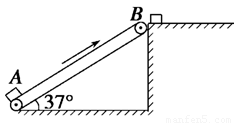
(1)每个工件从落上传送带的A点开始到被传送至最高点B所经历的时间;
(2)传送带对每个工件所做的功;
(3)由于传送工件,传送带的动力装置需增加的功率.
(1)6 s (2)24.32 J(3)14.72 W
【解析】
试题分析:(1)工件刚放上传送带时的加速度为
a=μgcos 37°-gsin 37°=0.4 m/s2 (2分)
当工件速度达v=0.8 m/s时,工件相对传送带静止
工件加速的时间t1=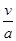 =
=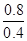 s=2
s (1分)
s=2
s (1分)
加速运动的位移
s1=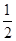 at12=
at12=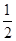 ×0.4×22 m=0.8 m (1分)
×0.4×22 m=0.8 m (1分)
在AB段匀速运动的位移为
s2=4 m-0.8 m=3.2 m (1分)
所用的时间为t2=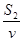 =
=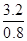 s=4
s (1分)
s=4
s (1分)
总时间为t=t1+t2=6 s (1分)
(2)由动能定理得
W-mgLsin 37°=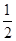 mv2
(3分)
mv2
(3分)
W=mgLsin 37°+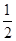 mv2
mv2
=1×10×4×0.6 J+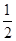 ×1×0.82 J=24.32
J (2分)
×1×0.82 J=24.32
J (2分)
(3)因工件在AB段上加速运动的时间为2 s,所以在位移xt内总是有一个工件位于传送带上,该工件对传送带的滑动摩擦力为Ff1=mgμcos 37°=6.4 N (2分)
工件在AB段上匀速运动过程中,因前后两工件相隔时间为2 s,两工件之间的距离为2×0.8 m=1.6 m,所以这段距离内始终有两个工件位于传送带上,每个工件对传送带的摩擦力为Ff2=mgsin 37°=6 N (3分)
传送带动力装置需增加的功率为
P=(Ff1+2Ff2)v=18.4×0.8 W=14.72 W (2分)
考点:牛顿第二定律 匀变速直线运动规律 动能定理

 作业辅导系列答案
作业辅导系列答案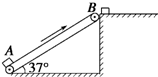 如图所示的传送带装置,长度为4m,与水平方向之间的夹角为37°,传送带以0.8m/s的速度匀速运行,从流水线上下来的工件每隔2s有一个落到A点(可认为初速度为零),工件质量为1kg.经传送带运送到与B等高处的平台上,再由工人运走.已知工件与传送带之间的动摩擦因数为μ=0.8,sin37°=0.6,cos37°=0.8,g=10m/s2.求:
如图所示的传送带装置,长度为4m,与水平方向之间的夹角为37°,传送带以0.8m/s的速度匀速运行,从流水线上下来的工件每隔2s有一个落到A点(可认为初速度为零),工件质量为1kg.经传送带运送到与B等高处的平台上,再由工人运走.已知工件与传送带之间的动摩擦因数为μ=0.8,sin37°=0.6,cos37°=0.8,g=10m/s2.求: