题目内容
3.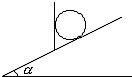 在倾角a=30°斜面上有块竖直放置的档板,在档板和斜面之间放有一个重为G=20N的光滑圆球,如图所示,试求:
在倾角a=30°斜面上有块竖直放置的档板,在档板和斜面之间放有一个重为G=20N的光滑圆球,如图所示,试求:(1)这个球对斜面的压力和对档板的压力.
(2)若挡板从该位置逆时针缓慢转动到水平位置,则球对斜面的压力和对档板的压力如何变化?
分析 (1)将小球的重力按作用效果进行分解,作出力图,根据数学知识求出球对斜面的压力和对档板的压力.
(2)在球所受的三个力中,重力大小方向都不变,斜面支持力方向不变,三力的合力为零,作出几个有代表性的图进行分析.
解答 解:(1)球受到竖直向下的重力作用,这个重力总是欲使球向下运动,但是由于挡板和斜面的支持,球才保持静止状态,因此,球的重力产生两个作用效果,如图所示,两个分力:①使球垂直压紧档板的力F1;②使球垂直压紧斜面的力F2,
将重力G分解为F1和F2,由几何知识可得 :
:
F1=Gtanα=20×tan30°=$\frac{20}{3}$$\sqrt{3}$N,
F2=$\frac{G}{cosα}$=$\frac{20}{cos30°}$=$\frac{40}{3}\sqrt{3}$N.
由牛顿第三定律可知,F1和F2分别等于球对挡板和斜面的压力.
(2)受力分析如图,将N1与N2合成,其合力与重力等大反向,
挡板转动时,挡板给球的弹力N1与斜面给球的弹力N2合力大小方向不变,其中N2的方向不变,作辅助图如上,挡板转动过程中,N1的方向变化如图中a、b、c的规律变化,为满足平行四边形定则,其大小变化规律为先变小后变大,其中挡板与斜面垂直时为最小;故N1先减小后增大,N2一直减小;
根据牛顿第三定律,知球对斜面的压力一直减小,对挡板的压力先减小后增大.
答:(1)这个球对斜面的压力是$\frac{40}{3}\sqrt{3}$N,对档板的压力是$\frac{20}{3}$$\sqrt{3}$N.
(2)挡板从该位置逆时针缓慢转动到水平位置,球对斜面的压力一直减小,对挡板的压力先减小后增大.
点评 本题关键是对小球受力分析,然后根据平衡条件并运用合成法分析;要明确三力平衡中,任意两个力的合力与第三个力等值、反向、共线.

 科技馆中的一个展品如图所示,在较暗处有一个不断均匀滴水的水龙头,在一种特殊的间歇闪光灯的照射下,若调节间歇闪光时间间隔正好与水滴从A下落到B的时间相同,可以看到一种奇特的现象,水滴似乎不再下落,而是像固定在图中的A、B、C、D四个位置不动,对出现的这种现象,下列描述正确的是(g=10m/s2)( )
科技馆中的一个展品如图所示,在较暗处有一个不断均匀滴水的水龙头,在一种特殊的间歇闪光灯的照射下,若调节间歇闪光时间间隔正好与水滴从A下落到B的时间相同,可以看到一种奇特的现象,水滴似乎不再下落,而是像固定在图中的A、B、C、D四个位置不动,对出现的这种现象,下列描述正确的是(g=10m/s2)( )| A. | 水滴在下落过程中通过相邻两点之间的时间满足tAB<tBC<tCD | |
| B. | 间歇发光的间隔时间是$\frac{\sqrt{2}}{10}$s | |
| C. | 水滴在相邻两点之间的平均速度vAB:vBC:vCD=1:4:9 | |
| D. | 水滴在各点速度之比满足vB:vC:vD=1:3:5 |
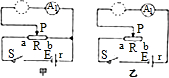
 利用如图所示装置可测磁感应强度,矩形线圈宽为L,共N匝,磁场垂直于纸面,当线圈中通以方向如图所示的电流I时,天平达到平衡状态.当电流改为反方向时(大小不变),右边再加质量为m的砝码后,天平重新平衡,由此可知( )
利用如图所示装置可测磁感应强度,矩形线圈宽为L,共N匝,磁场垂直于纸面,当线圈中通以方向如图所示的电流I时,天平达到平衡状态.当电流改为反方向时(大小不变),右边再加质量为m的砝码后,天平重新平衡,由此可知( )| A. | 磁感应强度的方向垂直纸面向里,大小为$\frac{{(m}_{1}+{m}_{2})g}{NIL}$ | |
| B. | 磁感应强度的方向垂直纸面向里,大小为$\frac{mg}{2NIL}$ | |
| C. | 磁感应强度的方向垂直纸面向外,大小为$\frac{({m}_{1}-{m}_{2})g}{NIL}$ | |
| D. | 磁感应强度的方向垂直纸面向外,大小为$\frac{mg}{2NIL}$ |
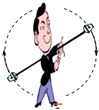 如图所示的杂技演员在表演水流星的节目时,手持两端系有盛水的杯子的绳子中点在竖直面内做圆周运动,若两只杯子内盛水的质量相等,当一只杯子在最高点时水恰好不洒出来,这时另一只杯子中的水对杯底的压力大小是水的重力的( )
如图所示的杂技演员在表演水流星的节目时,手持两端系有盛水的杯子的绳子中点在竖直面内做圆周运动,若两只杯子内盛水的质量相等,当一只杯子在最高点时水恰好不洒出来,这时另一只杯子中的水对杯底的压力大小是水的重力的( )| A. | 2倍 | B. | 4倍 | C. | 5倍 | D. | 6倍 |

| A. | t=1s时物体的加速度大小为1.0m/s2 | |
| B. | t=5s时物体的加速度大小为7.5m/s2 | |
| C. | 第3s内物体的位移为3m | |
| D. | 物体在加速过程的位移比减速过程的位移大 |
 某探究小组要尽可能精确地测量电流表
某探究小组要尽可能精确地测量电流表 的满偏电流,可供选用的器材如下
的满偏电流,可供选用的器材如下 (满偏电流Ig约为800μA,内阻r1约为100Ω)
(满偏电流Ig约为800μA,内阻r1约为100Ω) (量程为0.6A,内阻r2=0.1Ω)
(量程为0.6A,内阻r2=0.1Ω) (量程为3V,内阻RV=3kΩ)
(量程为3V,内阻RV=3kΩ)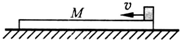 如图所示,一质量m=2kg的长木板静止在水平地面上,某时刻一质量M=1kg小铁块以水平向左的速度v0=9m/s从木板的右端滑上木板,已知木板与地面间的动摩擦因数μ1=0.1,铁块与木板间的动摩擦因数μ2=0.4,重力加速度g=10m/s2,木板足够长,求:
如图所示,一质量m=2kg的长木板静止在水平地面上,某时刻一质量M=1kg小铁块以水平向左的速度v0=9m/s从木板的右端滑上木板,已知木板与地面间的动摩擦因数μ1=0.1,铁块与木板间的动摩擦因数μ2=0.4,重力加速度g=10m/s2,木板足够长,求: 一长木板在水平地面上运动,在t=0时刻将一相对于地面静止的物块轻放到木板上,以后物块运动的速度-时间图象如图所示.己知物块与木板的质量相等,物块与木板间及木板与地面间均有摩擦,物块与木板间的最大静摩擦力等于滑动摩擦力,经0.5s木板前进S0=1.5m,且物块始终在木板上.取重力加速度的大小g=10m/s2,求:
一长木板在水平地面上运动,在t=0时刻将一相对于地面静止的物块轻放到木板上,以后物块运动的速度-时间图象如图所示.己知物块与木板的质量相等,物块与木板间及木板与地面间均有摩擦,物块与木板间的最大静摩擦力等于滑动摩擦力,经0.5s木板前进S0=1.5m,且物块始终在木板上.取重力加速度的大小g=10m/s2,求: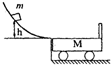 如图所示,光滑斜槽水平末端与停在光滑水平面上长为L=2.0m的小车上表面在同一水平面上,小车右端固定一个弹性挡板(即物体与挡板碰撞时无机械能损失).一个质量为m=1.0kg的小物块从斜槽上高h=1.25m处由静止滑下冲上小车,已知小车质量M=3.0kg,物块与小车间动摩擦因数为μ=0.45,g取l0m/s2.求整个运动过程中小车的最大速度.
如图所示,光滑斜槽水平末端与停在光滑水平面上长为L=2.0m的小车上表面在同一水平面上,小车右端固定一个弹性挡板(即物体与挡板碰撞时无机械能损失).一个质量为m=1.0kg的小物块从斜槽上高h=1.25m处由静止滑下冲上小车,已知小车质量M=3.0kg,物块与小车间动摩擦因数为μ=0.45,g取l0m/s2.求整个运动过程中小车的最大速度.