题目内容
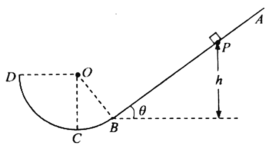
【题目】如图所示,斜面![]() 与半径为
与半径为![]() 的光滑竖直圆弧轨道
的光滑竖直圆弧轨道![]() 相切于B点,
相切于B点,![]() 与水平面之间的夹角为
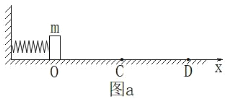
与水平面之间的夹角为![]() ,C为轨道的最低点,圆心O点与圆弧轨道最高点D在同一高度。现将一质量为
,C为轨道的最低点,圆心O点与圆弧轨道最高点D在同一高度。现将一质量为![]() 的小滑块从斜面上的P点由静止开始释放,P点与B点之间的高度差为
的小滑块从斜面上的P点由静止开始释放,P点与B点之间的高度差为![]() 。已知滑块与斜面之间的动摩擦因数
。已知滑块与斜面之间的动摩擦因数![]() ,
,![]() ,
,![]() ,
,![]() ,不计空气阻力。求:
,不计空气阻力。求:
(1)滑块第一次经过轨道最低点C时,对圆弧轨道的压力大小;
(2)滑块返回斜面时,沿斜面上滑的最大距离;
(3)滑块在斜面上运动的总路程。
【答案】(1)17N;(2)0.4m;(1)3m
【解析】
(1)滑块从P到C过程中,根据动能定理,有
![]()
在最低点C,支持力和重力的合力提供向心力,根据牛顿第二定律,有
![]()
代入数据解得
![]()
根据牛顿第三定律,滑块对圆弧轨道的压力与支持力等大反向,大小也是![]() ,方向竖直向下;
,方向竖直向下;
(2)滑块返回斜面时,设沿斜面上滑的最大距离为![]() ,由动能定理,有
,由动能定理,有
![]()
代入数据解得
![]()
(3) 物体在斜面上运动时机械能不断减小,在斜面上升的最大高度越来越小,最终在以B为一端点的圆弧上来回运动,设物块在斜面上运动的总路程为![]() ,由能量守恒,有
,由能量守恒,有
![]()
代入数据解得
![]()
答:(1)滑块第一次经过轨道最低点C时,对圆弧轨道的压力大小为![]() ;(2)滑块返回斜面时,沿斜面上滑的最大距离为
;(2)滑块返回斜面时,沿斜面上滑的最大距离为![]() ;(3) 滑块在斜面上运动的总路程为
;(3) 滑块在斜面上运动的总路程为![]() 。
。

练习册系列答案
相关题目