题目内容
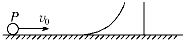
一质量为m的小球以v0的速度与静止在光滑水平面上的质量为M的小球发生对心碰撞，碰撞时无机械能损失.求碰后两球的速度.
解析：设碰后m的速度为v1,M的速度为v2,由动量守恒定律得
mv0=mv1+Mv2 ①
因碰撞时无机械能损失，总动能守恒
mv02=
mv12+
Mv22 ②
联立求解方程①、②便可得到v1、v2，但该二元二次方程组用代入法解很麻烦，需变形后再解
①变为m(v0-v1)=Mv2 ③
②变为
m(v02-v12)= 
Mv22 ④
④除以③得
v0+v1=v2 ⑤
解①⑤组成的方程组可得v1=
v0 ⑥
v2=
v0. ⑦
讨论:（1）m＞M时，v1为正；m＜M时，v1为负，
即被反向弹回；m=M时，v1=0,v2=v0，即碰后两球交换速度.
（2）当m＞＞M时，v1≈v0,v2≈2v0;
当m＜＜M时，v1≈-v0,v2≈0.
小学期末标准试卷系列答案
光滑的水平轨道AB，与半径为R的光滑的半圆形轨道BCD相切于B点，其中圆轨道在竖直平面内，B为最低点，D为最高点．一质量为m的小球以初速度v沿AB运动，恰能通过最高点，则（ ）
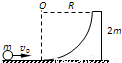
圆弧，圆弧半径为R=1m．一质量为m的小球以速度v向右运动冲上滑块．已知M=4m，g取10m/s2，若小球刚好没跃出圆弧的上端，求：