题目内容
光滑的水平轨道AB，与半径为R的光滑的半圆形轨道BCD相切于B点，其中圆轨道在竖直平面内，B为最低点，D为最高点．一质量为m的小球以初速度v沿AB运动，恰能通过最高点，则（ ）A．R越大，v越大
B．R越大，小球经过B点后的瞬间对轨道的压力越大
C．m越大，v越大
D．m与R同时增大，初动能Ek0增大
【答案】分析：小球恰能通过最高点时，由重力提供向心力，根据牛顿第二定律求出小球经最高点时的速度，根据动能定理求出初速度v与半径R的关系．小球经过B点后的瞬间由重力和轨道的支持力的合力提供向心力，由牛顿运动定律研究小球对轨道的压力与半径的关系．
解答：解：
A、C小球恰能通过最高点时，则有mg=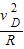
，
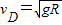，根据动能定理得，
=
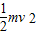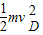+2mgR，得到
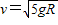，可见，R越大，v越大，而且v与小球的质量m无关．故A正确，C错误．
B、小球经过B点后的瞬间，N-mg=m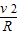
，得到轨道对小球的支持力N=mg+m
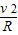，R越大，N越小，小球经过B点后的瞬间对轨道的压力也越小．故B错误．
D、初动能Ek0=
=
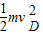+2mgR=
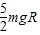，得知m与R同时增大，初动能Ek0增大．故D正确．
故选AD
点评：动能定理与向心力知识综合是常见的题型．小球恰好通过最高点时速度与轻绳模型类似，轨道对小球恰好没有作用力，由重力提供向心力，临界速度v=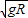
，做选择题时可直接运用．
解答：解：
A、C小球恰能通过最高点时，则有mg=
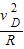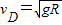，，根据动能定理得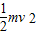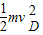，=+2mgR，得到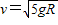，可见，R越大，v越大，而且v与小球的质量m无关．故A正确，C错误．B、小球经过B点后的瞬间，N-mg=m
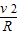，得到轨道对小球的支持力N=mg+m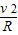，R越大，N越小，小球经过B点后的瞬间对轨道的压力也越小．故B错误．D、初动能Ek0=
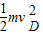=+2mgR=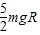，得知m与R同时增大，初动能Ek0增大．故D正确．故选AD
点评：动能定理与向心力知识综合是常见的题型．小球恰好通过最高点时速度与轻绳模型类似，轨道对小球恰好没有作用力，由重力提供向心力，临界速度v=
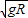，做选择题时可直接运用． 
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
如图所示，一个光滑的水平轨道AB与光滑的圆轨道BCD连接，其中圆轨道在竖直平面内，半径为R，B为最低点，D为最高点，一个质量为m的小球以初速度V0沿AB运动，刚好能通过最高点D，则（ ）
一个光滑的水平轨道AB与一光滑的圆形轨道BCDS相接，其中圆轨道在竖直平面内，D为最高点，B为最低点，半径为R，一质量为m的小球以初速度v0，沿AB运动，恰能通过最高点，则（ ）
（2008?徐州三模）光滑的水平轨道AB，与半径为R的光滑的半圆形轨道BCD相切于B点，其中圆轨道在竖直平面内，B为最低点，D为最高点．一质量为m的小球以初速度v0沿AB运动，恰能通过最高点，则（ ）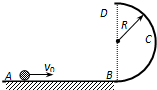
光滑的水平轨道AB，与半径为R的光滑的半圆形轨道BCD相切于B点，其中圆轨道在竖直平面内，B为最低点，D为最高点．为使一质量为m的小球以初速度v0沿AB运动，恰能通过最高点，则（ ）| A、R越小，v0越大 | B、m越大，v0越大 | C、R越大，小球经过B点后瞬间对轨道的压力越大 | D、小球经过B点后瞬间对轨道的压力与R无关 |
