题目内容
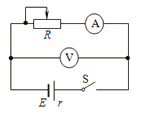
【题目】如图所示叠放在水平转台上的小物体A、B、C随转台一起以角速度ω匀速转动(各接触面均无相对滑动),A、B、C的质量分别为m、2m、3m,A与B、B与转台、C与转台间的动摩擦因数都为μ,B、C离转台中心的距离分别为r、1.5r.设最大静摩擦力等于滑动摩擦力.以下说法中正确的是( )
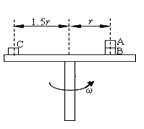
A. B、C两物体线速度大小之比为3:2
B. 转台的角速度一定满足:ω≤![]()
C. C与转台间的摩擦力大于A与B间的摩擦力
D. B与转台间的摩擦力可能达到3μmg
【答案】BC
【解析】由于BC两物体具有相同的角速度,半径之比为2:3,根据v=ωr可知,B、C两物体线速度大小之比为2:3,故A错误;对AB整体,有:(m+2m)ω2r≤μ(m+2m)g;对物体C,有:3mω2(1.5r)≤μ3mg;对物体A,有:mω2r≤μ(m)g;联立解得:ω≤![]() ,故B正确.由于A与C转动的角速度相同,由摩擦力提供向心力有3m×1.5rω2>mrω2,所以C与转台间的摩擦力大于A与B间的摩擦力,故C正确;若B与转台间的摩擦力达到3μmg,对AB整体,有:(m+2m)ω2r=μ(m+2m)g,解得:ω=
,故B正确.由于A与C转动的角速度相同,由摩擦力提供向心力有3m×1.5rω2>mrω2,所以C与转台间的摩擦力大于A与B间的摩擦力,故C正确;若B与转台间的摩擦力达到3μmg,对AB整体,有:(m+2m)ω2r=μ(m+2m)g,解得:ω=![]() ;对C物体,根据向心力公式可知C需要的向心力F=3mω2×1.5r=4.5mμg>3μmg,所以C物体不能相对转盘静止,故D错误;故选BC.
;对C物体,根据向心力公式可知C需要的向心力F=3mω2×1.5r=4.5mμg>3μmg,所以C物体不能相对转盘静止,故D错误;故选BC.

练习册系列答案
相关题目