题目内容
如所示，一细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处，细线的另一端拴一质量为m的小球．当滑块以a=2g的加速度向左运动时，线中拉力T等于多少？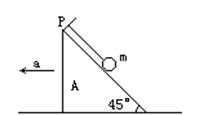
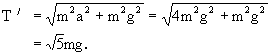
根据小球贴着滑块运动时的受力情况，可列出水平方向和竖直方向的运动方程分别为
Tcos45°-Nsin45°=ma， ①
Tsin45°+Ncos45°=mg． ②
联立两式，得N=mgcos45°-masin45°．
若小球对滑块的压力等于零，即应使N=0，滑块的加速度至少应为
可见，当滑块以a=2g加速向左运动时，小球已脱离斜面飘起．此时小球仅受两个力作用：重力mg、线中拉力T′（图3-40）．设线与竖直方向间夹角为β．同理由牛顿第二定律得
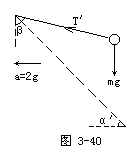
T′sinβ=ma，
T′cosβ=mg．
联立两式得
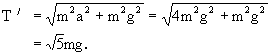
Tcos45°-Nsin45°=ma， ①
Tsin45°+Ncos45°=mg． ②
联立两式，得N=mgcos45°-masin45°．
若小球对滑块的压力等于零，即应使N=0，滑块的加速度至少应为
可见，当滑块以a=2g加速向左运动时，小球已脱离斜面飘起．此时小球仅受两个力作用：重力mg、线中拉力T′（图3-40）．设线与竖直方向间夹角为β．同理由牛顿第二定律得
T′sinβ=ma，
T′cosβ=mg．
联立两式得
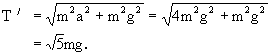
练习册系列答案
相关题目
v从木板的左端滑向右端，当木块m滑到木板M的右端
时，m的速度变为
，M、m间的动摩擦因数为μ，求