题目内容
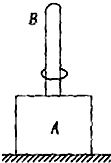如图所示，底座A上装有长0.5m的直立杆，其总质量为0.2kg，杆上套有质量为0.05kg的小环B，它与杆有摩擦．当环从座上以4m/s的速度起飞时，刚好能到达杆顶，求：（1）在环升起过程中，底座对水平面的压力多大？
（2）小环从杆顶落回底座需多长时间？（g=10m/s2）
分析：（1）根据速度位移公式求出环上升时的加速度大小，根据牛顿第二定律求出对环的阻力大小，在对A受力分析，运用共点力平衡求出底座对水平面的压力．
（2）根据牛顿第二定律求出环下滑时的加速度，再根据位移时间公式求出运动的时间．
（2）根据牛顿第二定律求出环下滑时的加速度，再根据位移时间公式求出运动的时间．
解答：解：（1）由v2=2ax得，a=
=16m/s2．
对B受力分析，由牛顿第二定律得，f+mBg=mBa，解得f=0.3N．
对A受力分析，由平衡条件得，N+f=mAg，解得N=1.7N．
由牛顿第三定律得，N′=N=1.7N．
（2）B下滑时对B受力分析，由牛顿第二定律得，mBg-f=mBa′
解得a′=
=4m/s2．
由x=
a′t2得，t=0.5s．
答：（1）在环升起过程中，底座对水平面的压力为1.7N．
（2）小环从杆顶落回底座需0.5s．
| v2 |
| 2s |
对B受力分析，由牛顿第二定律得，f+mBg=mBa，解得f=0.3N．
对A受力分析，由平衡条件得，N+f=mAg，解得N=1.7N．
由牛顿第三定律得，N′=N=1.7N．
（2）B下滑时对B受力分析，由牛顿第二定律得，mBg-f=mBa′
解得a′=
| mBg-f |
| mB |
由x=
| 1 |
| 2 |
答：（1）在环升起过程中，底座对水平面的压力为1.7N．
（2）小环从杆顶落回底座需0.5s．
点评：解决本题的关键知道加速度是联系前后的桥梁，根据加速度可以根据力求运动，也可以根据运动求力．
练习册系列答案
相关题目
如图所示，底座A上装有长0.5m的直立杆，总质量为0.2kg，杆上套有质量为0.05kg的小环B，它与杆之间有摩擦．若环从底座上以4m/s的初速度飞起，则刚好能到达杆顶．求：
如图所示，底座A上装有长0.5m的直立杆，其总质量为0.2kg，杆上套有0.05kg的小环B，与杆有摩擦．当环以4m/s的初速度从底座向上运动，刚好能到达杆顶（A始终处于静止状态）求：
如图所示，底座A上装有长s=0.5m的直立杆，质量M=0.2kg，杆上套有m=0.05kg的小环B，它与杆之间有摩擦．若环从底座上以v0=4m/s的速度飞起，刚好能到达杆顶（g=10m/s2）．下列说法错误的是（ ）
如图所示，底座A上装有长0.5m的直立杆，总质量为1kg，用细线悬挂，底座底面离水平地面H=0.2m，杆上套有质量为0.2kg的小环B，它与杆间有摩擦，设环与杆相对滑动时摩擦力大小始终不变，环从底座以