题目内容
2.做匀加速运动的列车出站后,车头经过某标牌时的速度为2m/s,车尾经过该牌时的速度为14m/s,则车身的中部经过该标牌时的速度大小为( )| A. | 10m/s | B. | 6m/s | C. | 8m/s | D. | 12m/s |
分析 列车出站做匀加速直线运动,车头经过站台和车尾经过站台,求车中部经过站台的速度,相当于求做匀加速直线运动的物体经过一段位移的初末速度求中间位移时的速度.
解答 解:列车经过站台,可看成匀加速直线运动的物体经过车头的速度为v0=1m/s,经过车尾的速度为v=7m/s,设经过列车中间位置时的速度vx
令列车长度为L,加速度为a,则据速度位移关系v2-v02=2ax得:
vx2-v02=2ax
v2-vx2=2a$\frac{L}{2}$
联立解得 vx=$\sqrt{\frac{{v}_{0}^{2}+{v}^{2}}{2}}$=$\sqrt{\frac{{2}^{2}+1{4}^{2}}{2}}$m/s=10m/s
故选:A
点评 把列车的运动看成一个质点匀加速运动一个列车长度,求质点在位移中点的瞬时速度,利用速度位移关系求解即可.

练习册系列答案
相关题目
12. 图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.若带电粒子在运动中只受电场力作用,根据此图可作出正确判断的是( )
图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.若带电粒子在运动中只受电场力作用,根据此图可作出正确判断的是( )
 图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.若带电粒子在运动中只受电场力作用,根据此图可作出正确判断的是( )
图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.若带电粒子在运动中只受电场力作用,根据此图可作出正确判断的是( )| A. | 带电粒子所带电荷的符号 | |
| B. | 带电粒子在a、b两点的受力方向 | |
| C. | 带电粒子在a、b两点的电势能何处较大 | |
| D. | 带电粒子一定由b向a方向运动 |
13.下列关于物体重心的说法中,正确的是( )
| A. | 物体的重心必在物体上 | |
| B. | 物体只在重心处受力,其他部分不受力 | |
| C. | 重心是物体各部分所受重力的合力的等效作用点 | |
| D. | 重心就是物体内最重的一点 |
7.某质点的速度图象如图所示,则下列说法中正确的是( )


| A. | 在0~6s内,质点做匀变速直线运动 | B. | 在6~14s内,质点做匀变速直线运动 | ||
| C. | 在6~10s内,质点做匀速直线运动 | D. | 在14s末,质点回到原位置 |
14.下列关于摩擦力和弹力的说法正确的是( )
| A. | 有摩擦力必有弹力 | |
| B. | 摩擦力的方向总是与物体运动方向相反 | |
| C. | 有弹力必有摩擦力 | |
| D. | 形变越大的物体产生的弹力越大 |
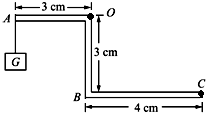 如图所示,有一弯曲的杠杆AOBC,O为支点,在A端挂一重为400N的物体,为了使杠杆在图中所示的位置平衡,加在C端最小的力是240N.
如图所示,有一弯曲的杠杆AOBC,O为支点,在A端挂一重为400N的物体,为了使杠杆在图中所示的位置平衡,加在C端最小的力是240N.

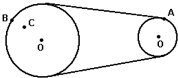 如图所示为一种常见的皮带传动装置的示意图,皮带传动后无打滑现象.已知A、B、C三点的半径RA=R,RB=2R,RC=$\frac{2R}{3}$,则A、B两点转动周期之比TA:TB:=1:2,而A、C两点向心加速度之比aA:aC=6:1.
如图所示为一种常见的皮带传动装置的示意图,皮带传动后无打滑现象.已知A、B、C三点的半径RA=R,RB=2R,RC=$\frac{2R}{3}$,则A、B两点转动周期之比TA:TB:=1:2,而A、C两点向心加速度之比aA:aC=6:1.