题目内容
一圆弧形的槽，槽底放在水平地面上，槽的两侧与光滑斜坡aa′、bb′相切，相切处a、b位于同一水平面内，槽与斜坡在竖直平面内的截面如图所示。一小物块从斜坡aa′上距水平面ab的高度为2h处沿斜坡自由滑下，并自a处进入槽内，到达b后沿斜坡bb′向上滑行，已知到达的最高处距水平面ab 的高度为h；接着小物块沿斜坡bb′滑下并从b处进入槽内反向运动，若不考虑空气阻力，则（ ）
| A．小物块再运动到a处时速度变为零 |
| B．小物块每次经过圆弧槽最低点时对槽的压力不同 |
| C．小物块不仅能再运动到a处，还能沿斜坡aa′向上滑行，上升的最大高度为h |
| D．小物块不仅能再运动到a处，还能沿斜坡aa′向上滑行，上升的最大高度小于h |
BD
试题分析：因要克服摩擦阻力做功，所以每次通过最低点的速度会变小，根据圆周运动公式及牛顿第二定律有
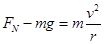，故可知物块与圆弧槽间的正压力会变小，所以B正确；设第一次通过圆弧槽过程中克服摩擦力做功为
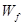，根据动能定理可得
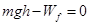，第二次通过圆弧槽的最低点时因正压力减小，所以摩擦力减小，同理，其它位置所对应的摩擦力都变小，故第二次通过圆弧槽克服摩擦力做的功将小于第一次，即
，所以D正确、AC错误；
练习册系列答案
名校课堂系列答案
相关题目
从O1点沿O1O2方向射出，恰能到达P点．不计重力，点电荷－q克服电场力做的功为W。若将－q换成+q，质量不变，仍以初速度
， 则( )
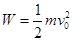
的均匀粗钢丝绳固定在等高的
、
处，钢丝绳最低点与固定点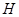
，动滑轮起点在
的人抓住滑轮下方的挂钩由
点，
，高度差为
．若参赛者在运动过程中始终处于竖直状态，抓住滑轮的手与脚底之间的距离也为
，滑轮与钢丝绳间的摩擦力大小视为不变，且摩擦力所做功与滑过的路程成正比，不计参赛者在运动中受到的空气阻力、滑轮（含挂钩）的质量和大小，不考虑钢索桥的摆动及形变．
、宽度为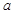
，厚度不计的海绵垫子上．若参赛者由
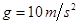，sin370=0.6,cos370=0.8。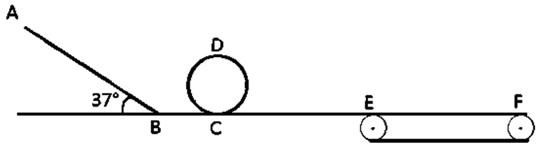
、电量
的可视为质点的带电小球与弹簧接触但不栓接。某一瞬间释放弹簧弹出小球，小球从水平台右端A点飞出，恰好能没有碰撞地落到粗糙倾斜轨道的最高B点，并沿轨道滑下。已知AB的竖直高度
，倾斜轨道与水平方向夹角为
、倾斜轨道长为
，带电小球与倾斜轨道的动摩擦因数
。倾斜轨道通过光滑水平轨道CD与光滑竖直圆轨道相连，在C点没有能量损失，所有轨道都绝缘，运动过程小球的电量保持不变。只有过山车模型的竖直圆轨道处在范围足够大竖直向下的匀强电场中，场强
。（cos37°=0.8，sin37°=0.6，取g=10m/s2）求：
，小球进入轨道后可以有多少次通过竖直圆轨道上距水平轨道高为0.01m的某一点P？
。求：
；
的匀强电场中，如图所示，斜面高为H，释放物体后，物块落地的速度大小为( )
