题目内容
20.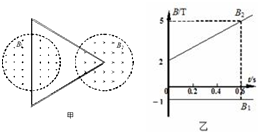 如图甲,固定在光滑水平面上的正三角形金属线框,匝数n=20,总电阻R=2.5Ω,边长L=0.3m.处在两个半径均为r=$\frac{L}{3}$的圆形匀强磁场区域中.线框顶点与右侧圆中心重合,线框底边中点与左侧圆中心重合.磁感应强度B1垂直水平面向外,大小不变;B2垂直水平面向里,大小随时间变化,B1、B2的值如图乙所示.(π取3)( )
如图甲,固定在光滑水平面上的正三角形金属线框,匝数n=20,总电阻R=2.5Ω,边长L=0.3m.处在两个半径均为r=$\frac{L}{3}$的圆形匀强磁场区域中.线框顶点与右侧圆中心重合,线框底边中点与左侧圆中心重合.磁感应强度B1垂直水平面向外,大小不变;B2垂直水平面向里,大小随时间变化,B1、B2的值如图乙所示.(π取3)( )| A. | 通过线框中感应电流方向为逆时针方向 | |
| B. | t=0时刻穿过线框的磁通量为0.1Wb | |
| C. | 在t=0.6s内通过线框中的电量为0.006C | |
| D. | 经过t=0.6s线框中产生的热量为0.06J |
分析 根据楞次定律判断感应电流的方向;根据磁通量Φ=BS求解;由q=n$\frac{△Φ}{R}$求解电荷量;由Q=I2Rt求解热量.
解答 解:A、由磁感应强度B1垂直水平面向外,大小不变;B2垂直水平面向里,大小随时间增大,故线框的磁通量减小,由楞次定律可得,线框中感应电流方向为逆时针方向,故A正确;
B、t=0时刻穿过线框的磁通量为:∅=B1×$\frac{1}{2}$×πr2-B2×$\frac{1}{6}$×πr2=1×0.5×3×0.12-2×$\frac{1}{6}$×3×0.12Wb=0.005Wb,故B错误;
C、在t=0.6s内通过线框中的电量q=n$\frac{△Φ}{R}$=$\frac{20×(5-2)×\frac{1}{6}×3×0.{1}^{2}}{2.5}$C=0.12C,故C错误;
D、线框产生的感应电动势 E=n$\frac{△Φ}{△t}$=20×$\frac{(5-2)×\frac{1}{6}×3×0.{1}^{2}}{0.6}$V=0.5V
感应电流 I=$\frac{E}{R}$=$\frac{0.5}{2.5}$=0.2A
由Q=I2Rt=0.22×2.5×0.6J=0.06J,故D正确.
故选:AD.
点评 此题考查磁通量的定义,注意磁通量的正负,理解法拉第电磁感应定律与闭合电路欧姆定律的应用,及其焦耳定律,注意安培力大小计算与方向的判定.

练习册系列答案
相关题目
11. 如图所示,空间存在足够大、正交的匀强电、磁场,电场强度为E、方向竖直向下,磁感应强度为B、方向垂直纸面向里.从电、磁场中某点P由静止释放一个质量为m、带电量为+q的粒子(粒子受到的重力忽略不计),其运动轨迹如图虚线所示,对于带电粒子在电、磁场中下落的最大高度H,下面给出了四个表达式,用你已有的知识计算可能会有困难,但你可以用学过的知识对下面的四个选项做出判断,你认为正确的是( )
如图所示,空间存在足够大、正交的匀强电、磁场,电场强度为E、方向竖直向下,磁感应强度为B、方向垂直纸面向里.从电、磁场中某点P由静止释放一个质量为m、带电量为+q的粒子(粒子受到的重力忽略不计),其运动轨迹如图虚线所示,对于带电粒子在电、磁场中下落的最大高度H,下面给出了四个表达式,用你已有的知识计算可能会有困难,但你可以用学过的知识对下面的四个选项做出判断,你认为正确的是( )
 如图所示,空间存在足够大、正交的匀强电、磁场,电场强度为E、方向竖直向下,磁感应强度为B、方向垂直纸面向里.从电、磁场中某点P由静止释放一个质量为m、带电量为+q的粒子(粒子受到的重力忽略不计),其运动轨迹如图虚线所示,对于带电粒子在电、磁场中下落的最大高度H,下面给出了四个表达式,用你已有的知识计算可能会有困难,但你可以用学过的知识对下面的四个选项做出判断,你认为正确的是( )
如图所示,空间存在足够大、正交的匀强电、磁场,电场强度为E、方向竖直向下,磁感应强度为B、方向垂直纸面向里.从电、磁场中某点P由静止释放一个质量为m、带电量为+q的粒子(粒子受到的重力忽略不计),其运动轨迹如图虚线所示,对于带电粒子在电、磁场中下落的最大高度H,下面给出了四个表达式,用你已有的知识计算可能会有困难,但你可以用学过的知识对下面的四个选项做出判断,你认为正确的是( )| A. | $\frac{mB}{2Eq}$ | B. | $\frac{mE}{2{B}^{2}q}$ | C. | $\frac{2mB}{{E}^{2}q}$ | D. | $\frac{2mE}{{B}^{2}q}$ |
8.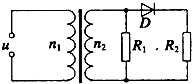 如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=11:5,电阻R1=R2=25Ω,D为理想二极管,原线圈接u=220$\sqrt{2}$sin100πt(V)的交流电.则( )
如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=11:5,电阻R1=R2=25Ω,D为理想二极管,原线圈接u=220$\sqrt{2}$sin100πt(V)的交流电.则( )
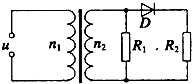 如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=11:5,电阻R1=R2=25Ω,D为理想二极管,原线圈接u=220$\sqrt{2}$sin100πt(V)的交流电.则( )
如图所示的电路中,理想变压器原、副线圈的匝数比n1:n2=11:5,电阻R1=R2=25Ω,D为理想二极管,原线圈接u=220$\sqrt{2}$sin100πt(V)的交流电.则( )| A. | 用交流电流表测得通过R1的电流为4A | |
| B. | 用交流电流表测得通过R2的电流为$\sqrt{2}$A | |
| C. | 变压器的输入功率为600W | |
| D. | 副线圈中电流的有效值为6A |
15.下列说法正确的是( )
| A. | 分子间存在引力,使液体分子间保持一定的间隙 | |
| B. | 气体的温度越高,某速率区间分子占总分子数的百分率一定越大 | |
| C. | 液晶分子没有固定的位置,但排列有大致相同的取向 | |
| D. | 蜘蛛网上挂着的小露珠呈球状属于毛细现象 |
5.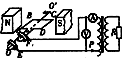 如图所示,矩形线圈ABCD绕垂直于磁场的轴OO′匀速转动,矩形线圈通过滑环与理想变压器相连,触头P可移动,电表均为理想交流电表.已知:矩形线圈面积为0.01m2,内阻为5Ω,匝数为125匝,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\sqrt{2}$T,副线圈所接电阻R=30Ω.当线圈平面与磁场方向平行时开始计时,下列说法正确的是( )
如图所示,矩形线圈ABCD绕垂直于磁场的轴OO′匀速转动,矩形线圈通过滑环与理想变压器相连,触头P可移动,电表均为理想交流电表.已知:矩形线圈面积为0.01m2,内阻为5Ω,匝数为125匝,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\sqrt{2}$T,副线圈所接电阻R=30Ω.当线圈平面与磁场方向平行时开始计时,下列说法正确的是( )
 如图所示,矩形线圈ABCD绕垂直于磁场的轴OO′匀速转动,矩形线圈通过滑环与理想变压器相连,触头P可移动,电表均为理想交流电表.已知:矩形线圈面积为0.01m2,内阻为5Ω,匝数为125匝,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\sqrt{2}$T,副线圈所接电阻R=30Ω.当线圈平面与磁场方向平行时开始计时,下列说法正确的是( )
如图所示,矩形线圈ABCD绕垂直于磁场的轴OO′匀速转动,矩形线圈通过滑环与理想变压器相连,触头P可移动,电表均为理想交流电表.已知:矩形线圈面积为0.01m2,内阻为5Ω,匝数为125匝,转动的角速度为100rad/s,匀强磁场的磁感应强度为$\sqrt{2}$T,副线圈所接电阻R=30Ω.当线圈平面与磁场方向平行时开始计时,下列说法正确的是( )| A. | 线圈中感应电动势的表达式为e=125$\sqrt{2}$cos(100t)V | |
| B. | P上移电流表读数不变 | |
| C. | 当原副线圈匝数比为2:1时,电流表示数为$\sqrt{2}$A | |
| D. | 当原副线圈匝数比为2:1时,电阻R上消耗的功率为120W |
12.学习物理除了学习学科知识外,还要了解物理学家在物理概念的建立、物理规律的发现过程中运用的思想与方法.关于以上两点下列叙述正确的是( )
| A. | 在验证力的平行四边形定则的实验中使用了控制变量的方法 | |
| B. | 质点和点电荷都是理想化模型,实际运用时分别代替实际物体和带电体 | |
| C. | 库仑提出了用电场线描述电场的方法 | |
| D. | 奥斯特发现了电磁感应现象,进一步揭示了电现象与磁现象间的联系 |
10.“天宫一号”在其设计寿命结束后,将在指令控制下坠落地球.已知天宫一号的运行轨道高度在与飞船交会对接时大约距离大气层340km;无人期间则会适当调高,约370km.则下列判断中正确的是( )
| A. | 航天员在天宫一号内处于不受地球万有引力的状态 | |
| B. | 天宫一号的运行速度大于7.9km/s,小于11.2km/s | |
| C. | 天宫一号在对接高度处的运行速度比无人期间的轨道上的运行速度大 | |
| D. | 天宫一号坠落地球的过程中机械能不断减少,速度也会越来越小 |
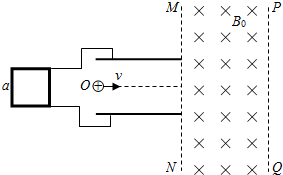 如图所示,一边长a=0.2m的1000匝导线框,线框内部加有垂直线框平面的均匀变化的匀强磁场.线框两端通过导线与一间距为d=0.24m的垂直纸面放置的平行板电容器连接,电容器右侧的边界MN右侧空间加有一电场强度为E=100V/m的匀强电场(图中未标出).一质量为m、电荷量为q=5×10-6C的带正电的微粒从板的左端中点O以速度v=0.5m/s水平射入极板间,恰好沿直线通过极板,并垂直进入左边界为MN、右边界为PQ的宽为L=0.4m的匀强磁场,恰能做匀速圆周运动.磁场方向垂直纸面向里,磁感应强度B0=10T.已知g=10m/s2.
如图所示,一边长a=0.2m的1000匝导线框,线框内部加有垂直线框平面的均匀变化的匀强磁场.线框两端通过导线与一间距为d=0.24m的垂直纸面放置的平行板电容器连接,电容器右侧的边界MN右侧空间加有一电场强度为E=100V/m的匀强电场(图中未标出).一质量为m、电荷量为q=5×10-6C的带正电的微粒从板的左端中点O以速度v=0.5m/s水平射入极板间,恰好沿直线通过极板,并垂直进入左边界为MN、右边界为PQ的宽为L=0.4m的匀强磁场,恰能做匀速圆周运动.磁场方向垂直纸面向里,磁感应强度B0=10T.已知g=10m/s2.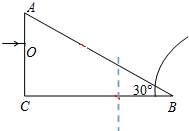 如图所示,直角三棱镜折射率为$\sqrt{2}$,∠B=30°,一束单色光垂直于AC面射向棱镜,入射点为O,试画出光在棱镜中传播的光路图,并求出光射出棱镜时折射角.(不考虑BC面对光线的反射)
如图所示,直角三棱镜折射率为$\sqrt{2}$,∠B=30°,一束单色光垂直于AC面射向棱镜,入射点为O,试画出光在棱镜中传播的光路图,并求出光射出棱镜时折射角.(不考虑BC面对光线的反射)