题目内容
【题目】一个质量为m电荷量为q的带电粒子从x轴上的P（a，0）点以速度v，沿与x正方向成60°的方向射入第一象限内的匀强磁场中，并恰好垂直于y轴射出第一象限。求：
(1)判断粒子的电性；
(2)匀强磁场的磁感应强度B和射出点的坐标。
(3)带电粒子在磁场中的运动时间是多少？
【答案】(1)负电 (2)坐标为
(3)
【解析】
(1)粒子进入磁场受洛伦兹力作用偏转，由左手定则可知，离子带负电；
(2)由几何轨迹找到圆心位置，由几何关系得到半径，洛伦兹力提供向心力，由牛顿第二定律列方程可得匀强磁场的磁感应强度B；根据几何知识求得粒子射出点离O点的距离．
(3)根据粒子在磁场中转过的圆心角与粒子做圆周运动的周期求出粒子在磁场中的运动时间．
(1) 粒子进入磁场受洛伦兹力作用偏转，由左手定则可知，粒子带负电
(2)设磁感应强度为B，粒子在磁场中做匀速圆周运动的半径为r.
由
由射入、射出点的半径可找到圆心O′，粒子在磁场中运动情况如图：
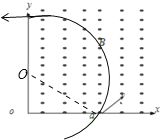
由几何知识有
联立解得:
又由几何知识知
出射点到O点的距离为
所以出射点的坐标为：
(3)设粒子在磁场中做匀速圆周运动的周期为T,则
由图知，粒子在磁场中做圆周运动对应的圆心角为
所以，粒子在磁场中运动的时间是
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
