题目内容
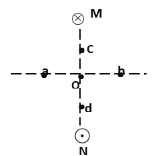
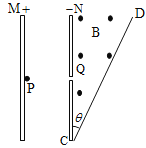
【题目】如图所示，M、N为两块带等量异种电荷的平行金属板，两板间电压可取从零到某一最大值之间的各种数值。静止的带电粒子带电荷量为＋q，质量为m（不计重力），从点P经电场加速后，从小孔Q进入N板右侧的匀强磁场区域，磁感应强度大小为B，方向垂直于纸面向外，CD为磁场边界上的一绝缘板，它与N板的夹角为θ＝30°，孔Q到板的下端C的距离为L，当M、N两板间电压取最大值时，粒子恰垂直打在CD板上，则下列说法正确的是
A．两板间电压的最大值
B．CD板上可能被粒子打中区域的长度
C．粒子在磁场中运动的最长时间
D．能打到N板上的粒子的最大动能为
【答案】ACD
【解析】
试题据题，M、N两板间电压取最大值时，粒子恰垂直打在CD板上，所以其轨迹圆心在C点，CH=QC=L，故轨迹半径R1=L
又由牛顿第二定律得
粒子在MN间加速时，有
所以联立得
，选项A正确；
打在QC间的粒子在磁场中运动的时间最长，均为半周期．粒子运动的周期为
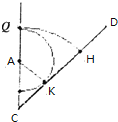
所以最长时间
，选项C正确；设轨迹与CD板相切于K点，半径为R2，在△AKC中：
可得 
,即KC长等于 
, 所以CD板上可能被粒子打中的区域即为HK的长度，
，选项B错误；能达到N板上的粒子最大半径为R2，根据
，最大动能为：
，选项D正确；故选ACD．
练习册系列答案
相关题目
