题目内容
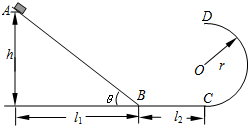 如图所示,斜面与水平面在B点衔接,水平面与竖直面内的半圆形导轨在C点衔接,半圆形导轨的半径为r=0.4m.质量m=0.50kg的小物块,从A点沿斜面由静止开始下滑,测得它经过C点进入半圆形导轨瞬间对导轨的压力为35N,之后向上运动恰能完成半圆周运动到达D点.已知A到B的水平距离为l1=3.2m,B到C的水平距离为l2=1.6m,物块与斜面及水平面之间的动摩擦因数均为μ=0.25,不计物块通过衔接点时的能量损失,g取10m/s2.
如图所示,斜面与水平面在B点衔接,水平面与竖直面内的半圆形导轨在C点衔接,半圆形导轨的半径为r=0.4m.质量m=0.50kg的小物块,从A点沿斜面由静止开始下滑,测得它经过C点进入半圆形导轨瞬间对导轨的压力为35N,之后向上运动恰能完成半圆周运动到达D点.已知A到B的水平距离为l1=3.2m,B到C的水平距离为l2=1.6m,物块与斜面及水平面之间的动摩擦因数均为μ=0.25,不计物块通过衔接点时的能量损失,g取10m/s2.求:
(1)物块从C至D克服阻力做了多少功?
(2)A点离水平面的高度h为多大?
(3)为使物块恰好不能越过C而进入半圆形导轨内,物块在斜面上下滑的起始高度应调节为多大?
分析:(1)小球经过C点时由重力和轨道的支持力的合力提供向心力,根据牛顿第二定律求出小球经过C点的速度.小球恰好到达D点时,由重力提供向心力,求出小球经过D点的速度,再根据动能定理求解物块从C至D克服阻力做功.
(2)从A到B过程,由动能定理求出h.
(3)物块恰好不能越过C点时速度为零,再由动能定理求解物块在斜面上下滑的起始高度.
(2)从A到B过程,由动能定理求出h.
(3)物块恰好不能越过C点时速度为零,再由动能定理求解物块在斜面上下滑的起始高度.
解答:解:(1)圆周运动在C点有,N-mg=m
①
圆周运动在D点有,mg=m
②
从C至D由动能定理有,-mg?2r-Wf=
m
-
m
③
联立①②③式并代入数据可解得,从C至D物块克服阻力做的功Wf=1J ④
(2)从A到B过程,物块克服阻力做的功W1=μmgcosθ?
=μmgl1 ⑤
从A到C,由动能定理有,mgh-W1-μmgl2=
m
-0⑥
联立①⑤⑥式并代入数据可解得,h=2.4m⑦
(3)从起始到C点由动能定理有,mgh′-μmgcosθ?
-μmgl2=0⑧
又
=
=
⑨
联立⑧⑨式并代入数据可解得,h'=0.6m
答:
(1)物块从C至D克服阻力做了1J功.
(2)A点离水平面的高度h为2.4m.
(3)为使物块恰好不能越过C而进入半圆形导轨内,物块在斜面上下滑的起始高度应调节为0.6m.
| ||
| r |
圆周运动在D点有,mg=m
| ||
| r |
从C至D由动能定理有,-mg?2r-Wf=
| 1 |
| 2 |
| v | 2 D |
| 1 |
| 2 |
| v | 2 C |
联立①②③式并代入数据可解得,从C至D物块克服阻力做的功Wf=1J ④
(2)从A到B过程,物块克服阻力做的功W1=μmgcosθ?
| l1 |
| cosθ |
从A到C,由动能定理有,mgh-W1-μmgl2=
| 1 |
| 2 |
| v | 2 C |
联立①⑤⑥式并代入数据可解得,h=2.4m⑦
(3)从起始到C点由动能定理有,mgh′-μmgcosθ?
| h′ |
| sinθ |
又
| sinθ |
| cosθ |
| h′ |
| l1 |
| 3 |
| 4 |
联立⑧⑨式并代入数据可解得,h'=0.6m
答:
(1)物块从C至D克服阻力做了1J功.
(2)A点离水平面的高度h为2.4m.
(3)为使物块恰好不能越过C而进入半圆形导轨内,物块在斜面上下滑的起始高度应调节为0.6m.
点评:物块做圆周运动时,根据向心力知识求解速度,根据动能定理求解阻力做功,都是常用的方法和思路.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
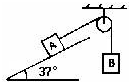
 如图所示,斜面与水平面的夹角为37°,物体A质量为2kg,与斜面间摩擦因数为0.4,求:
如图所示,斜面与水平面的夹角为37°,物体A质量为2kg,与斜面间摩擦因数为0.4,求: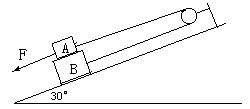 如图所示,斜面与水平方向成
如图所示,斜面与水平方向成