题目内容
如图所示,光滑轨道的DP段为水平轨道,PQ段为半径是R的竖直半圆轨道,半圆轨道的下端与水平的轨道的右端相切于P点,一轻质弹簧左端A固定,另一端拴接一个质量为m的小球B,质量也为m的小球C靠在B球的右侧,现用外力作用在C上,使弹簧被压缩了0.4R(弹簧仍在弹性限度内).这时小球静止于距离P端3R的水平轨道上,若撤去外力,C球运动到轨道的最高点Q后又恰好落回到原出发点.已知重力加速度为g.求

(1)小球C运动到Q点时对轨道的压力多大?
(2)撤去外力前的瞬间,弹簧的弹性势能EP是多少?

(1)小球C运动到Q点时对轨道的压力多大?
(2)撤去外力前的瞬间,弹簧的弹性势能EP是多少?
分析:(1))弹簧和B、C两个球的组成的系统能量守恒,B、C脱离弹簧时,弹簧的弹性势能转化为B、C球的动能,C球在运动的过程中机械能守恒,离开Q点之后C球做的是平抛运动,由平抛运动的规律可以求得小球在Q点的速度的大小,从而由牛顿第二定律可以求得C球到Q点时对轨道的压力.
(2)撤去外力前的瞬间,弹簧的弹性势能作用下,B、C两球获得动能,因此借助平抛运动求出C球抛出速度,再由机械能守恒算出小球C被弹出的速度,从而根据能量守恒,确定撤去外力时弹簧的弹性势能.
(2)撤去外力前的瞬间,弹簧的弹性势能作用下,B、C两球获得动能,因此借助平抛运动求出C球抛出速度,再由机械能守恒算出小球C被弹出的速度,从而根据能量守恒,确定撤去外力时弹簧的弹性势能.
解答:解:(1)设小球经过最高点Q时的速度为v,
由平抛规律有:竖直方向 2R=
gt2
水平方向:3R=vt
联立两式得:v=
小球C在最高点,由牛顿第二定律得:FN+mg=m
解得:FN=
mg
(2)设小球C离开小球B时的速度为v0,只有重力做功,小球机械能守恒.
由机械能守恒有:
m
=
mv2+2mgR
弹簧恢复到原长时脱离,则由能量守恒有:EP=
×2m
联立上述各式得:EP=
mgR
答:(1)小球C运动到Q点时对轨道的压力
mg;
(2)撤去外力前的瞬间,弹簧的弹性势能EP是
mgR.
由平抛规律有:竖直方向 2R=
| 1 |
| 2 |
水平方向:3R=vt
联立两式得:v=
| 3 |
| 2 |
| gR |
小球C在最高点,由牛顿第二定律得:FN+mg=m
| v2 |
| R |
解得:FN=
| 5 |
| 4 |
(2)设小球C离开小球B时的速度为v0,只有重力做功,小球机械能守恒.
由机械能守恒有:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
弹簧恢复到原长时脱离,则由能量守恒有:EP=
| 1 |
| 2 |
| v | 2 0 |
联立上述各式得:EP=
| 5 |
| 2 |
答:(1)小球C运动到Q点时对轨道的压力
| 5 |
| 4 |
(2)撤去外力前的瞬间,弹簧的弹性势能EP是
| 5 |
| 2 |
点评:本题考查了能量的转化和守恒,同时还有机械能守恒和平抛运动的规律,涉及的知识点较多,对学生的能力要求较高.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
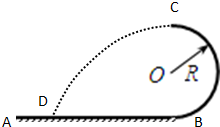 如图所示,光滑轨道的AB段为水平面,BC段为竖直面内的半圆弧,圆弧的半径R=2.5m,有一小球沿此轨道从水平面以一定速度冲上圆弧,刚好通过最高点C后,沿水平方向抛出,落到地面上的D点,g=10m/s2.求:
如图所示,光滑轨道的AB段为水平面,BC段为竖直面内的半圆弧,圆弧的半径R=2.5m,有一小球沿此轨道从水平面以一定速度冲上圆弧,刚好通过最高点C后,沿水平方向抛出,落到地面上的D点,g=10m/s2.求: 如图所示,光滑轨道的DP段为水平轨道,PQ段为半径是R的竖直半圆轨道,半圆轨道的下端与水平的轨道的右端相切于P点.一轻质弹簧两端分别固定质量为2m的小球A和质量为m的小球B,质量为m小球C靠在B球的右侧.现用外力作用在A和C上,弹簧被压缩(弹簧仍在弹性限度内).这时三个小球均静止于距离P端足够远的水平轨道上.若撤去外力,C球恰好可运动到轨道的最高点Q.已知重力加速度为g.求:
如图所示,光滑轨道的DP段为水平轨道,PQ段为半径是R的竖直半圆轨道,半圆轨道的下端与水平的轨道的右端相切于P点.一轻质弹簧两端分别固定质量为2m的小球A和质量为m的小球B,质量为m小球C靠在B球的右侧.现用外力作用在A和C上,弹簧被压缩(弹簧仍在弹性限度内).这时三个小球均静止于距离P端足够远的水平轨道上.若撤去外力,C球恰好可运动到轨道的最高点Q.已知重力加速度为g.求: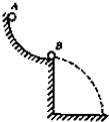 如图所示,光滑轨道的下端离地0.8m,质量为m的A球从轨道上端无初速释放,到下端时与质量也为m的B球正碰,B球碰后做平抛运动,落地点与抛出点的水平距离为0.8m,则A球释放的高度h可能是
如图所示,光滑轨道的下端离地0.8m,质量为m的A球从轨道上端无初速释放,到下端时与质量也为m的B球正碰,B球碰后做平抛运动,落地点与抛出点的水平距离为0.8m,则A球释放的高度h可能是