题目内容
 (2012?泗县模拟)如图所示,光滑轨道的DP段为水平轨道,PQ段为半径是R的竖直半圆轨道,半圆轨道的下端与水平的轨道的右端相切于P点,一轻质弹簧左端A固定,另一端拴接一个质量为m的小球B,质量也为m的小球C靠在B球的右侧,现用外力作用在C上,使弹簧被压缩了0.4R(弹簧仍在弹性限度内).这时小球静止于距离P端3R的水平轨道上,若撤去外力,C球运动到轨道的最高点Q后又恰好落回到原出发点.已知重力加速度为g.求撤去外力前的瞬间,弹簧的弹性势能EP是多少?
(2012?泗县模拟)如图所示,光滑轨道的DP段为水平轨道,PQ段为半径是R的竖直半圆轨道,半圆轨道的下端与水平的轨道的右端相切于P点,一轻质弹簧左端A固定,另一端拴接一个质量为m的小球B,质量也为m的小球C靠在B球的右侧,现用外力作用在C上,使弹簧被压缩了0.4R(弹簧仍在弹性限度内).这时小球静止于距离P端3R的水平轨道上,若撤去外力,C球运动到轨道的最高点Q后又恰好落回到原出发点.已知重力加速度为g.求撤去外力前的瞬间,弹簧的弹性势能EP是多少?分析:弹簧和bc两个球的组成的系统能量守恒,bc脱离弹簧时,弹簧的弹性势能转化为bc球的动能,c球在运动的过程中机械能守恒,离开Q点之后c球做的是平抛运动,由平抛运动的规律可以求得小球在Q点的速度的大小,从而可以求得c球的动能的大小.
解答:解:外力撤出后,弹簧恢复原长时,设B、C共同速度为VP,
由能量守恒有 EP=2×
m
,
此后B、C分离,设C运动至最高点Q时速度为V,由机械能守恒得:
mg?2R+
mV2=
m
,
小球C由Q落到原出发点做平抛运动,
3R=Vt
2R=
gt2
联立以上方程可以解得EP=
mgR=6.25mgR.
所以弹簧的弹性势能EP是6.25mgR.
由能量守恒有 EP=2×
| 1 |
| 2 |
| V | 2 P |
此后B、C分离,设C运动至最高点Q时速度为V,由机械能守恒得:
mg?2R+
| 1 |
| 2 |
| 1 |
| 2 |
| V | 2 P |
小球C由Q落到原出发点做平抛运动,
3R=Vt
2R=
| 1 |
| 2 |
联立以上方程可以解得EP=
| 25 |
| 4 |
所以弹簧的弹性势能EP是6.25mgR.
点评:本题考查了能量的转化和守恒,同时还有机械能守恒和平抛运动的规律,涉及的知识点较多,对学生的能力要求较高.

练习册系列答案
相关题目
 (2012?泗县模拟)如图所示,在同一轨道平面上的几个人造星球卫星A、B、C,在某一时刻恰好在同一条直线上,下列说法中正确的是( )
(2012?泗县模拟)如图所示,在同一轨道平面上的几个人造星球卫星A、B、C,在某一时刻恰好在同一条直线上,下列说法中正确的是( )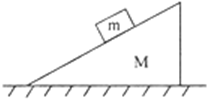 (2012?泗县模拟)质量为m的物体,沿质量为M的固定斜面匀速下滑,如图,斜面的倾角为θ,则下列说法正确的是( )
(2012?泗县模拟)质量为m的物体,沿质量为M的固定斜面匀速下滑,如图,斜面的倾角为θ,则下列说法正确的是( )