题目内容
10. 如图所示,比荷为$\frac{e}{m}$的电子,以速度v0沿AB边射入边长为a的等边三角形的匀强磁场区域中,欲使电子从BC边穿出,磁感应强度B的取值应小于$\frac{\sqrt{3}m{v}_{0}}{ea}$.
如图所示,比荷为$\frac{e}{m}$的电子,以速度v0沿AB边射入边长为a的等边三角形的匀强磁场区域中,欲使电子从BC边穿出,磁感应强度B的取值应小于$\frac{\sqrt{3}m{v}_{0}}{ea}$.
分析 电子进入磁场后受到洛伦兹力作用而做匀速圆周运动,由半径公式r=$\frac{mv}{qB}$知,电子的速率越大,轨迹半径越大,欲使电子能经过BC边,当电子恰好从C点离开时,轨迹半径最小,由几何知识求出最小的半径,由半径公式求出B的最大值,即可得到B的范围.
解答 解:电子在磁场中做匀速圆周运动,洛伦兹力提供向心力,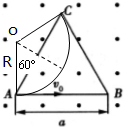
由牛顿第二定律得:evB=m$\frac{{v}_{0}^{2}}{r}$,解得:r=$\frac{m{v}_{0}}{eB}$;
当电子从c点离开磁场时,电子做匀速圆周运动对应的半径最小,如图;
由几何知识得:2rcos30°=a,解得:r=$\frac{\sqrt{3}}{3}$a,
欲使电子能经过BC边,必须满足:r>$\frac{\sqrt{3}}{3}$a,
解得:B<$\frac{\sqrt{3}m{v}_{0}}{ea}$;
故答案为:小于$\frac{\sqrt{3}m{v}_{0}}{ea}$.
点评 本题是磁场中临界条件问题,关键是运用几何知识求最小的轨迹半径,即可由半径求解B的范围.

练习册系列答案
相关题目
20.下面的几个速度中表示平均速度的是( )
| A. | 子弹射出枪口的速度是800m/s | |
| B. | 以 790m/s的速度击中目标 | |
| C. | 汽车从甲站行驶到乙站的速度是40km/h | |
| D. | 汽车通过站牌时的速度是72km/h |
1.下列有关时间与时刻、位移与路程的说法中正确的是( )
| A. | 第5 s末到第7 s初是1 s的时间 | |
| B. | 时刻就是很短的时间 | |
| C. | 沿直线运动的物体,位移和路程总是相等的 | |
| D. | 物体位移的大小总是小于或等于路程 |
19.甲、乙两个物体在同一直线上沿正方向运动,a甲=6m/s2,a乙=-8m/s2,那么对甲、乙两物体判断正确的是( )
| A. | 甲的加速度大于乙的加速度 | |
| B. | 甲做减速直线运动,乙做加速直线运动 | |
| C. | 甲的速度比乙的速度变化慢 | |
| D. | 甲在相等时间内速度变化比乙大 |
1.在双缝干涉实验中,光屏上P点到双缝S1、S2距离之差△S1=0.75μm,光屏上Q点到双缝S1、S2距离之差△S2=1.5μm,若用频率为6.0×1014Hz的黄光照射双缝,则( )
| A. | P点出现明条纹,Q点出现暗条纹 | B. | Q点出现明条纹,P点出现暗条纹 | ||
| C. | 两点均出现明条纹 | D. | 两点均出现暗条纹 |

 如图,圆形水平转台半径R=0.5m,上表面离水平地面的高度H=l.25m,小物块 A位于转台边缘,与转台中心O距离r=0.3m的小物块B用水平细线与过O点的竖直转轴相连,A、B能随转台一起绕转轴转动,当转台的角速度ω=4rad/s时,物块A刚好要滑离转台、细线断裂,此时转台立即停止转动,设物块所受的最大静摩擦力等于滑动摩擦力,小物块B与转台的动摩擦因素μB=0.1,取g=l0m/s2.求:
如图,圆形水平转台半径R=0.5m,上表面离水平地面的高度H=l.25m,小物块 A位于转台边缘,与转台中心O距离r=0.3m的小物块B用水平细线与过O点的竖直转轴相连,A、B能随转台一起绕转轴转动,当转台的角速度ω=4rad/s时,物块A刚好要滑离转台、细线断裂,此时转台立即停止转动,设物块所受的最大静摩擦力等于滑动摩擦力,小物块B与转台的动摩擦因素μB=0.1,取g=l0m/s2.求: