题目内容
如图,水平面上有一带圆弧形光滑凸起的长方形木块A,木块A上的物体B用轻绳绕过凸起与物体C相连,B与凸起之间的绳是水平的。A与B之间动摩擦因数为μ1=0.8,A与地面之间的动摩擦因数为μ2=0.25。现用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,且C上方的悬线与竖直方向始终成37°角。物体A、B、C的质量分别为m、3m、2m,重力加速度为g,求:
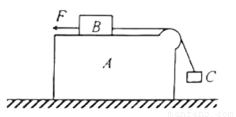
(1)拉力F的大小;
(2)两个接触面上的摩擦力的大小之比。
【答案】
【解析】
试题分析:(1)对A、B、C整体,受力分析可知:F—μ26mg=6ma ①
对C物体:Tcos37°=2mg ②
Tsin37°=2ma ③
解得:T=2.5mg ④
a=0.75g ⑤
⑤代入①,可得:F=6mg ⑥
(2)对B物体:F—T>3ma, 所以A与B之间的静摩擦力fAB 方向向右
F—T —fAB =3ma ⑦
⑤代入⑦,可得:fAB =1.25mg ⑧
A与地面间的滑动摩擦力f滑=μ26mg=1.5mg ⑨
由⑧、⑨可知,上下两个接触面上的摩擦力之比为5:6 ⑩
考点:牛顿第二定律,物体受力分析

练习册系列答案
相关题目
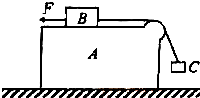 (2008?四川)水平面上有一带圆弧形凸起的长方形木块A,木块A上的物体B用绕过凸起的轻绳与物体C相连,B与凸起之间的绳是水平的.用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,如图.已知物体A、B、C、的质量均为m,重力加速度为g,不计所有的摩擦,则拉力F应为多大?
(2008?四川)水平面上有一带圆弧形凸起的长方形木块A,木块A上的物体B用绕过凸起的轻绳与物体C相连,B与凸起之间的绳是水平的.用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,如图.已知物体A、B、C、的质量均为m,重力加速度为g,不计所有的摩擦,则拉力F应为多大?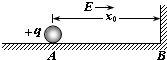 如图所示,在光滑水平面上有一带电量为+q,质量为m的带电小球,置于场强为E、方向水平向右的匀强电场中的A处,沿水平方向距A为x0的B处固定一个挡板,释放小球后,小球与挡板发生无能量损失碰撞,若每次碰撞中小球都有一半的电量损失(设挡板B始终不带电),则第二次碰撞后,小球离开B板的最大距离是( )
如图所示,在光滑水平面上有一带电量为+q,质量为m的带电小球,置于场强为E、方向水平向右的匀强电场中的A处,沿水平方向距A为x0的B处固定一个挡板,释放小球后,小球与挡板发生无能量损失碰撞,若每次碰撞中小球都有一半的电量损失(设挡板B始终不带电),则第二次碰撞后,小球离开B板的最大距离是( )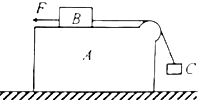 如图,水平面上有一带圆弧形光滑凸起的长方形木块A,木块A上的物体B用轻绳绕过凸起与物体C相连,B与凸起之间的绳是水平的.A与B之间动摩擦因数为μ1=0.8,A与地面之间的动摩擦因数为μ2=0.25.现用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,且C上方的悬线与竖直方向始终成37°角.物体A、B、C的质量分别为m、3m、2m,重力加速度为g,求:
如图,水平面上有一带圆弧形光滑凸起的长方形木块A,木块A上的物体B用轻绳绕过凸起与物体C相连,B与凸起之间的绳是水平的.A与B之间动摩擦因数为μ1=0.8,A与地面之间的动摩擦因数为μ2=0.25.现用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,且C上方的悬线与竖直方向始终成37°角.物体A、B、C的质量分别为m、3m、2m,重力加速度为g,求: 如图,在光滑水平面上有一带电量为-q,质量为m的带电小球,置于场强为E方向水平向右的匀强电场中的A处,沿水平方向距A为x0的B处固定一个挡板,释放小球后,小球与挡板发生无能量损失碰撞,若每次碰撞中小球都有一半的电量损失(设B始终不带电),则第二次碰撞后,小球离开板的最大距离是
如图,在光滑水平面上有一带电量为-q,质量为m的带电小球,置于场强为E方向水平向右的匀强电场中的A处,沿水平方向距A为x0的B处固定一个挡板,释放小球后,小球与挡板发生无能量损失碰撞,若每次碰撞中小球都有一半的电量损失(设B始终不带电),则第二次碰撞后,小球离开板的最大距离是