题目内容
3.游乐场的过山车可以底朝上在圆轨道上运行,游客却不会掉下来,如图1所示.我们把这种情形抽象成为如图2的模型:弧形轨道的下端与竖直圆轨道相接,使小球从弧形轨道上端滚下,并进入到圆形轨道内运动.实验发现,h较小时,小球到不了圆轨道的最高点,也不会脱离圆形轨道;h较大时,小球可以顺利通过圆形轨道的最高点而在竖直面内做完整的圆周运动.不考虑各种阻力的作用,小球视为质量为m的质点,圆轨道的半径为R.问:
(1)h满足什么条件时,小球可以顺利通过圆形轨道的最高点而在竖直面内做完整的圆周运动?
(2)h满足什么条件时,小球到不了圆轨道的最高点,也不会脱离圆形轨道,在此条件下,小球对圆形轨道的最低点的最大压力是多少?
分析 (1)小球不脱离轨道有两种情形:一种小球能通过最高点做完整的圆周运动.另一种小球下半个圆轨道上来回运动.当小球恰能通过最高点时由重力作为向心力,由向心力的公式可以求得小球通过最高点的临界速度,再由机械能守恒可以求得离地面的高度h.
(2)当小球恰好通过与轨道圆心等高位置时速度为零,由机械能守恒求此时的h,即可得到h的范围,结合机械能守恒求出此时小球的速度,再由向心力的表达式即可求出.
解答 解:(1)设小球能经过最高点,且过最高点时的速度为v,
在最高点$F+mg=m\frac{v^2}{R}$
小球能过最高点,应满足:F≥0
从释放到小球运动到圆轨道的最高点的过程中$mgh=\frac{1}{2}m{v^2}+mg•2R$
解得:$h≥\frac{5}{2}R$
(2)小球在圆轨道内上升的高度不超过圆心,则小球就不会脱轨,所以h≤R.
当h=R时,小球过最低点时速度最大,对轨道的压力最大,从释放到最低点的过程中,$\frac{1}{2}mv_1^2=mgR$
式中v1为h=R时小球经过圆轨道最低点时的速度.
在最低点:${F_{max}}-mg=m\frac{v_1^2}{R}$
解得:Fmax=3mg
答:(1)当满足$h≥\frac{5}{2}R$时,小球可以顺利通过圆形轨道的最高点而在竖直面内做完整的圆周运动;
(2)当满足h≤R时,小球到不了圆轨道的最高点,也不会脱离圆形轨道,在此条件下,小球对圆形轨道的最低点的最大压力是3mg.
点评 本题属于圆周运动中绳的模型,在最高点时应该是重力恰好作为圆周运动的向心力,对于圆周运动中的两种模型一定要牢牢的掌握.

练习册系列答案
相关题目
13.一个从静止开始做匀加速直线运动的物体,从开始运动起连续通过三段位移的时间分别是1s、2s、3s,下列选项中正确的是( )
| A. | 这三段位移的长度之比1:22:32 | |
| B. | B.这三段位移的长度之比1:23:33 | |
| C. | 这三段位移上的平均速度之比1:2:3 | |
| D. | 这三段位移上的平均速度之比1:22:32 |
11.第一次用水平恒力F作用在物体上,使物体在光滑水平面上移动距离l,F做功W1,第二次用同样大的力F沿斜面方向作用于物体上,使物体沿粗糙斜面移动的距离也是l,F做功W2,那么( )
| A. | W1>W2 | B. | W1=W2 | C. | W1<W2 | D. | 无法判断 |
15.下列关于我国照明电路所用的标准交流电压及频率正确的是( )
| A. | 电压有效值为220V,频率50Hz | B. | 电压有效值为$220\sqrt{2}$V,频率50Hz | ||
| C. | 电压有效值为220V,频率0.02Hz | D. | 电压有效值为$220\sqrt{2}$V,频率0.02Hz |
12. 如图所示,先闭合开关,保持平行板电容器始终与电源正负极相接.再由静止释放电子,电子从A板向B板运动,当到达B板时速度为v,则( )
如图所示,先闭合开关,保持平行板电容器始终与电源正负极相接.再由静止释放电子,电子从A板向B板运动,当到达B板时速度为v,则( )
 如图所示,先闭合开关,保持平行板电容器始终与电源正负极相接.再由静止释放电子,电子从A板向B板运动,当到达B板时速度为v,则( )
如图所示,先闭合开关,保持平行板电容器始终与电源正负极相接.再由静止释放电子,电子从A板向B板运动,当到达B板时速度为v,则( )| A. | 当增大两板间距离时,v增大 | |
| B. | 当减小两板间距离时,v增大 | |
| C. | 当增大两板间距离时,电容器的电量增大 | |
| D. | 当减小两板间距离时,电容器的电量增大 |
9. 如图所示,水平放置的两平行金属板长为L、间距为L,有一质量为m、电荷量为q 的带正电小球从原点沿x 轴正方向进入两金属板间.当小球运动到点($\frac{2L}{3}$,$\frac{L}{2}$)处时,在两金属板间加一恒定电压U,使小球开始做匀速直线运动,取重力加速度为g,不计空气阻力,下列说法中正确的是( )
如图所示,水平放置的两平行金属板长为L、间距为L,有一质量为m、电荷量为q 的带正电小球从原点沿x 轴正方向进入两金属板间.当小球运动到点($\frac{2L}{3}$,$\frac{L}{2}$)处时,在两金属板间加一恒定电压U,使小球开始做匀速直线运动,取重力加速度为g,不计空气阻力,下列说法中正确的是( )
 如图所示,水平放置的两平行金属板长为L、间距为L,有一质量为m、电荷量为q 的带正电小球从原点沿x 轴正方向进入两金属板间.当小球运动到点($\frac{2L}{3}$,$\frac{L}{2}$)处时,在两金属板间加一恒定电压U,使小球开始做匀速直线运动,取重力加速度为g,不计空气阻力,下列说法中正确的是( )
如图所示,水平放置的两平行金属板长为L、间距为L,有一质量为m、电荷量为q 的带正电小球从原点沿x 轴正方向进入两金属板间.当小球运动到点($\frac{2L}{3}$,$\frac{L}{2}$)处时,在两金属板间加一恒定电压U,使小球开始做匀速直线运动,取重力加速度为g,不计空气阻力,下列说法中正确的是( )| A. | 小球初速度大小为$\frac{2}{3}$$\sqrt{gL}$ | |
| B. | 两金属板间所加电压大小为$\frac{mgL}{2q}$ | |
| C. | 小球最终从点(L,L)处射出金属板 | |
| D. | 小球最终落在下金属板上的点(L,$\frac{5}{6}L$)位置处 |
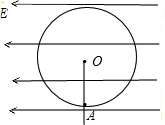 如图所示,水平向左的匀强电场中,用长为l的绝缘轻质细绳悬挂一小球,小球质量为m,带电量为+q,将小球拉至竖直位置最低位置A点处无初速释放,小球将向左摆动,细线向左偏高竖直方向的最大角度θ=74°.
如图所示,水平向左的匀强电场中,用长为l的绝缘轻质细绳悬挂一小球,小球质量为m,带电量为+q,将小球拉至竖直位置最低位置A点处无初速释放,小球将向左摆动,细线向左偏高竖直方向的最大角度θ=74°.