题目内容
一电梯,启动后匀加速上升,加速度为2m/s2,制动后匀减速上升,加速度大小为1m/s2,楼高54m.
(1)若上升的最大速度为6m/s,电梯上升到楼顶的时间是多少?
(2)如果电梯先加速上升,然后匀速上升最后减速上升至停止,全程共用时间为16.5s,上升的最大速度是多少?
(3)请用速度-时间图象描述第(2)问中的电梯的运动过程.
(1)若上升的最大速度为6m/s,电梯上升到楼顶的时间是多少?
(2)如果电梯先加速上升,然后匀速上升最后减速上升至停止,全程共用时间为16.5s,上升的最大速度是多少?
(3)请用速度-时间图象描述第(2)问中的电梯的运动过程.
分析:(1)电梯匀加速上升的过程,已知初速度、末速度和加速度,根据v=v0+at和v2-
=2ax求解出时间和位移;
匀减速过程同样根据v=v0+at和v2-
=2ax求解出时间和位移;最后得到匀速的位移,从而得到时间.
(2)设最大速度为v,根据第一问的思路,分别得到加速、减速和匀速的时间(包含v的表达式),最后代入数据求解;
(3)先建立坐标系,横轴表示时间,纵轴表示速度,然后画出t=0时刻、t=2s时刻、t=12.5s时刻和16.5s时刻的四个点,最后连成图象.
| v | 2 0 |
匀减速过程同样根据v=v0+at和v2-
| v | 2 0 |
(2)设最大速度为v,根据第一问的思路,分别得到加速、减速和匀速的时间(包含v的表达式),最后代入数据求解;
(3)先建立坐标系,横轴表示时间,纵轴表示速度,然后画出t=0时刻、t=2s时刻、t=12.5s时刻和16.5s时刻的四个点,最后连成图象.
解答:解:(1)电梯加速上升阶段:
时间t1=
=
s=3s
上升高度x1=
=
m=9m
电梯减速上升阶段:
时间t2=
=
s=6s
上升高度x1=
=
m=18m
电梯匀速上升的高度x3=54-9-18=27m
匀速上升时间t3=
=
s=4.5s
电梯上升的总时间:t=t1+t2+t3=3s+6s+4.5s=13.5s
即电梯上升到楼顶的时间是13.5s.
(2)由上述分析可知:
加速阶段:x1=
=
,时间t1=
=
减速阶段:x1=
=
,时间t2=
=
=v
匀速阶段:x3=v(t-t1-t2)=v(t-
-v)=v(t-
)
电梯上升的总高度:x=x1+x2+x3=
+
+v(t-
)
代入数值:54=
+
+v(16.5-
)
整理后:v2-22v+72=0
解得结果:v1=4m/s,v2=13m/s(舍去)
即电梯上升的最大速度是4m/s.
(3)速度图象如图所示
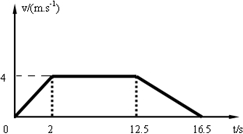
时间t1=
| v |
| a |
| 6 |
| 2 |
上升高度x1=
| v2 |
| 2a |
| 36 |
| 2×2 |
电梯减速上升阶段:
时间t2=
| v |
| a |
| 6 |
| 1 |
上升高度x1=
| v2 |
| 2a |
| 36 |
| 2×1 |
电梯匀速上升的高度x3=54-9-18=27m
匀速上升时间t3=
| x3 |
| v |
| 27 |
| 6 |
电梯上升的总时间:t=t1+t2+t3=3s+6s+4.5s=13.5s
即电梯上升到楼顶的时间是13.5s.
(2)由上述分析可知:
加速阶段:x1=
| v2 |
| 2a1 |
| v2 |
| 4 |
| v |
| a1 |
| v |
| 2 |
减速阶段:x1=
| v2 |
| 2a2 |
| v2 |
| 2 |
| v |
| a2 |
| v |
| 1 |
匀速阶段:x3=v(t-t1-t2)=v(t-
| v |
| 2 |
| 3v |
| 2 |
电梯上升的总高度:x=x1+x2+x3=
| v2 |
| 4 |
| v2 |
| 2 |
| 3v |
| 2 |
代入数值:54=
| v2 |
| 4 |
| v2 |
| 2 |
| 3v |
| 2 |
整理后:v2-22v+72=0
解得结果:v1=4m/s,v2=13m/s(舍去)
即电梯上升的最大速度是4m/s.
(3)速度图象如图所示

点评:本题关键要理清电梯的运动过程,然后分段对电梯运动过程运用v=v0+at和v2-
=2ax两个公式列式求解,同时要注意各段的时间、速度、位移要用下标加以区分.
| v | 2 0 |

练习册系列答案
相关题目