��Ŀ����
����Ϊm=1kg��С����������ˮƽ�����˶��Ĵ��ʹ��ϵ�P�㣬�洫�ʹ��˶���A���ˮƽ�׳���С���ǡ������ײ����Բ�����ߴ�B�������ֱ�⻬��Բ�¹���»���B��CΪԲ�������˵㣬������ˮƽ����֪Բ���뾶R=1.0mԲ����ӦԲ�ĽǦ�=106�㣬�����͵�ΪO��A���ˮƽ��ĸ߶�h=0.8m��С����뿪C���ǡ������ײ���ع̶�б�������˶���0.8s��D�㣬�����б���Ķ�Ħ������Ϊ��1=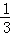 ��g=10m/s2��sin37��=0.6��cos37��=0.8������
��g=10m/s2��sin37��=0.6��cos37��=0.8������
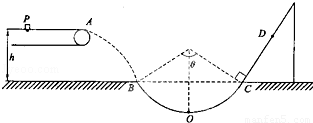
��1��С����뿪A��ʱ��ˮƽ���ٶ�v1��
��2��С��龭��O��ʱ�Թ����ѹ����
��3������С����봫�ʹ���Ķ�Ħ������Ϊ��2=0.3�����ʹ����ٶ�Ϊ5m/s����PA��ľ����Ƕ��٣�
��4��б����CD��ľ��룮
��1��3m/s����2��43N����3��1.5m��4��0.98m
��������
���������
��1����С��飬��A��B��vy2=2gh
��B��tan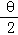 =
=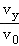
����v0=3m/s��
��2����С��飬��B��O�ɶ��ܶ����ɵã�
mgR��1��sin37�㣩=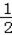 m
m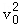 ��
��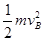
����vB=5m/s
��O��N��mg= 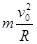
����N=43N
��ţ�ٵ�������֪�Թ����ѹ��ΪN��=43N
��3�����ʹ����ٶ�Ϊ5m/s������С����ڴ��ʹ���һֱ���٣�
��2mg=ma3
PA��ľ�����SPA=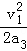 =1.5m
=1.5m
��4�������б���ϻ���mgsin53��+��mgcos53��=ma1
����a1=10m/s2
�����б���»���mgsin53�㩁��mgcos53��=ma2 ��ã�a2=6m/s2
�ɻ�е���غ�֪vc=vB=5m/s
С�����C��������ߵ���ʱt1= 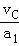 =0.5s
=0.5s
С�������ߵ�ص�D����ʱt2=0.8s��0.5s=0.3s
��SCD=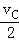 t1��
t1��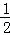 a2
a2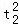
��SCD=0.98m��
���㣺ţ�ٶ��ɼ����ܶ������ۺ�Ӧ�á�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� ��ͼ��ʾ���⻬ˮƽ���Ͼ�ֹ���ų�L=1m������ΪM=3kg��ľ�飬һ������Ϊm=1kg��С���壨�ɿ����ʵ㣩����ľ������Ҷˣ�m��M֮��Ķ�Ħ��������=0.1�����ľ��ʩ��һˮƽ���ҵ�����F����gȡ10m/s2��
��ͼ��ʾ���⻬ˮƽ���Ͼ�ֹ���ų�L=1m������ΪM=3kg��ľ�飬һ������Ϊm=1kg��С���壨�ɿ����ʵ㣩����ľ������Ҷˣ�m��M֮��Ķ�Ħ��������=0.1�����ľ��ʩ��һˮƽ���ҵ�����F����gȡ10m/s2��
 ��ͼ��ʾ��������ľШ�����ڴֲ�ˮƽ�����ϣ�ľШ����M=9kg����Ǧ�=30�㣬������ľШ��б������һ������Ϊm=1kg��С��飮���������ٶ�ȡg=10m/s2��
��ͼ��ʾ��������ľШ�����ڴֲ�ˮƽ�����ϣ�ľШ����M=9kg����Ǧ�=30�㣬������ľШ��б������һ������Ϊm=1kg��С��飮���������ٶ�ȡg=10m/s2�� ��2008?�Ĵ�����ͼ��һ����Ϊm=1kg��ľ�徲ֹ�ڹ⻬ˮƽ�����ϣ���ʼʱ��ľ���Ҷ���ǽ���L=0.08m������Ϊm=1kg ��С����Գ��ٶ�v0=2m/s ����ľ����ˣ�ľ�峤�ȿɱ�֤������˶������в���ǽ�Ӵ��������ľ��֮��Ķ�Ħ������Ϊ��=0.1��ľ����ǽ����ײ����ȫ���Եģ�ȡg=10m/s2����
��2008?�Ĵ�����ͼ��һ����Ϊm=1kg��ľ�徲ֹ�ڹ⻬ˮƽ�����ϣ���ʼʱ��ľ���Ҷ���ǽ���L=0.08m������Ϊm=1kg ��С����Գ��ٶ�v0=2m/s ����ľ����ˣ�ľ�峤�ȿɱ�֤������˶������в���ǽ�Ӵ��������ľ��֮��Ķ�Ħ������Ϊ��=0.1��ľ����ǽ����ײ����ȫ���Եģ�ȡg=10m/s2���� ��ͼ��ʾ����Ϊ
��ͼ��ʾ����Ϊ