题目内容
2.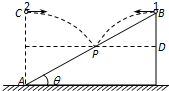 如图所示,长度为L、倾角θ=30°的斜面AB,在斜面顶端B向左水平抛出小球1、同时在底端A正上方某高度处水平向右抛出小球2,小球2垂直撞在斜面上的位置P,小球1也同时落在P点.求两球平抛的初速度v1、v2和BD间距离h.
如图所示,长度为L、倾角θ=30°的斜面AB,在斜面顶端B向左水平抛出小球1、同时在底端A正上方某高度处水平向右抛出小球2,小球2垂直撞在斜面上的位置P,小球1也同时落在P点.求两球平抛的初速度v1、v2和BD间距离h.
分析 两个小球同时做平抛运动,又同时落在P点,说明运动时间相同,即BC在同一水平面上,小球2垂直撞在斜面上的位置P上说方向与斜面明小球2的末速度垂直,可以根据几何关系求出相应的物理量.
解答  解:设运动时间为t、小球1和2的初速度为v1和v2、B球下落高度为h,小球1做平抛运动落在斜面上,有tanθ=$\frac{{y}_{1}}{{x}_{1}}$
解:设运动时间为t、小球1和2的初速度为v1和v2、B球下落高度为h,小球1做平抛运动落在斜面上,有tanθ=$\frac{{y}_{1}}{{x}_{1}}$
又x1=v1t,y1=$\frac{1}{2}$gt2,
解得tanθ=$\frac{gt}{2{v}_{1}}$ ①
小球2垂直撞在斜面上,有tanθ=$\frac{{v}_{2}}{{v}_{y}}$,即tanθ=$\frac{{v}_{2}}{gt}$ ②
根据几何关系有x1+x2=Lcos θ,即(v1+v2)t=Lcos θ ③
联立①②得v2•2v1=tan2θ ④
①③联立得2v1(v1+v2)tan θ=gLcos θ ⑤
④⑤联立解得v1=$\frac{3}{2}\sqrt{\frac{gL}{5}}$、v2=$\sqrt{\frac{gL}{5}}$
代入③解得t=$\sqrt{\frac{3L}{5g}}$
则下落高度h=y1=$\frac{1}{2}g{t}^{2}$=0.3L.
答:两球平抛的初速度v1、v2分别为$\frac{3}{2}\sqrt{\frac{gL}{5}}$和$\sqrt{\frac{gL}{5}}$.BD间距离h是0.3L.
点评 对于平抛运动,要熟练运用分解法研究,同时要抓住两个球之间的关系,如位移关系、时间关系等.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
8.做匀加速直线运动的物体,依次通过A、B、C三点,位移XAB=XBC,已知物体在AB段的平均速度为8m/s,在BC段的平均速度为12m/s,那么物体在B点时的瞬时速度的大小为( )
| A. | 10.0m/s | B. | 10.4m/s | C. | 10.6m/s | D. | 10.8m/s |
13.以下说法中正确的是( )
| A. | 物体的形状发生变化,重心的位置一定改变 | |
| B. | 当物体速度为零时,物体一定处于平衡状态 | |
| C. | 存在摩擦力的接触面间一定存在弹力 | |
| D. | 物体的运动方向一定是物体所受合外力的方向 |
7.两个共点力的合力最大为28N,最小为4N.则这两个力的大小和如果这两个力的夹角为90°合力的大小分别为( )
| A. | 12N,16N,20N | B. | 16N,12N,25N | C. | 18N,14N,20N | D. | 16N,12N,20N |
14.以下说法正确的是( )
| A. | 电磁波是一种物质,可以在真空中传播 | |
| B. | 磁场中两条磁感线一定不相交,但可以相切 | |
| C. | 首先发现通电导线周围存在磁场的物理学家是特斯拉 | |
| D. | 当一段导线在磁场中运动时,则导线中不一定有感应电流,但一定有感应电动势 |
11.如图所示为一质点做直线运动的v-t图象,下列说法中正确的是( )


| A. | 整个运动过程中,质点在C点的状态所对应的位置离出发点最远 | |
| B. | 整个运动过程中,BC段的加速度最大 | |
| C. | 整个运动过程中,CE段的加速度最大 | |
| D. | OA段所表示的运动通过的路程是25m |
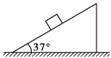 如图所示,在倾角为37°的固定斜面上静置一个质量为5kg的物体,物体与斜面间的动摩擦因数为0.8,若用原长为10cm,劲度系数为2×103N/m的弹簧沿斜面拉物体,使之沿斜面匀速运动,则弹簧的最终长度是多少?(取g=10m/s2)
如图所示,在倾角为37°的固定斜面上静置一个质量为5kg的物体,物体与斜面间的动摩擦因数为0.8,若用原长为10cm,劲度系数为2×103N/m的弹簧沿斜面拉物体,使之沿斜面匀速运动,则弹簧的最终长度是多少?(取g=10m/s2)