题目内容
20.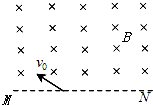 如图所示,界面MN上部为磁感应强度大小为B的匀强磁场,有一质量为m(不计重力),电量为q的负电荷,以v0的速度沿与MN成30°方向进入该匀强磁场,电荷进出匀强磁场两点之间距离d=$\frac{m{v}_{0}}{qB}$,电荷在匀强磁场中运动时间t=$\frac{5πm}{3qB}$.
如图所示,界面MN上部为磁感应强度大小为B的匀强磁场,有一质量为m(不计重力),电量为q的负电荷,以v0的速度沿与MN成30°方向进入该匀强磁场,电荷进出匀强磁场两点之间距离d=$\frac{m{v}_{0}}{qB}$,电荷在匀强磁场中运动时间t=$\frac{5πm}{3qB}$.
分析 电荷在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律求出电荷做圆周运动的轨道半径,然后求出两点间的距离;根据电荷在磁场中转过的圆心角与电荷做圆周运动的周期可以求出电荷在磁场中运动的时间.
解答  解:电荷在磁场中做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
解:电荷在磁场中做圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
qv0B=m$\frac{{v}_{0}^{2}}{r}$,
解得:r=$\frac{m{v}_{0}}{qB}$,
由几何知识可知,电荷出射点距离入射点距离:
d=2rsin30°=r=$\frac{m{v}_{0}}{qB}$,
电荷在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$,
电荷在磁场中的运动时间:
t=$\frac{θ}{360°}$T=$\frac{360°-60°}{360°}$×$\frac{2πm}{qB}$=$\frac{5πm}{3qB}$;
故答案为:$\frac{m{v}_{0}}{qB}$,$\frac{5πm}{3qB}$.
点评 本题考查了电荷在磁场中的运动,分析清楚电荷的运动过程、作出电荷的运动轨迹是正确解题的关键,应用牛顿第二定律与电荷的周期公式可以解题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
3.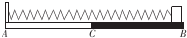 如图所示,AB为固定水平长木板,长为L,C为长木板的中点,AC段光滑,CB段粗糙,一原长为$\frac{L}{4}$的轻弹簧一端连在长木板左端的挡板上,一端连一物块,开始时将物块拉至长木板的右端B点,由静止释放物块,物块在弹簧弹力的作用下向左滑动,已知物块与长板间的动摩擦因数为u,物块的质量为m,弹簧的劲度系数为k,且k>$\frac{4μmg}{L}$,物块第一次到达c点时,物块的速度大小为vo,这时弹簧的弹性势能为E0,不计物块的大小,则下列说法正确的是( )
如图所示,AB为固定水平长木板,长为L,C为长木板的中点,AC段光滑,CB段粗糙,一原长为$\frac{L}{4}$的轻弹簧一端连在长木板左端的挡板上,一端连一物块,开始时将物块拉至长木板的右端B点,由静止释放物块,物块在弹簧弹力的作用下向左滑动,已知物块与长板间的动摩擦因数为u,物块的质量为m,弹簧的劲度系数为k,且k>$\frac{4μmg}{L}$,物块第一次到达c点时,物块的速度大小为vo,这时弹簧的弹性势能为E0,不计物块的大小,则下列说法正确的是( )
 如图所示,AB为固定水平长木板,长为L,C为长木板的中点,AC段光滑,CB段粗糙,一原长为$\frac{L}{4}$的轻弹簧一端连在长木板左端的挡板上,一端连一物块,开始时将物块拉至长木板的右端B点,由静止释放物块,物块在弹簧弹力的作用下向左滑动,已知物块与长板间的动摩擦因数为u,物块的质量为m,弹簧的劲度系数为k,且k>$\frac{4μmg}{L}$,物块第一次到达c点时,物块的速度大小为vo,这时弹簧的弹性势能为E0,不计物块的大小,则下列说法正确的是( )
如图所示,AB为固定水平长木板,长为L,C为长木板的中点,AC段光滑,CB段粗糙,一原长为$\frac{L}{4}$的轻弹簧一端连在长木板左端的挡板上,一端连一物块,开始时将物块拉至长木板的右端B点,由静止释放物块,物块在弹簧弹力的作用下向左滑动,已知物块与长板间的动摩擦因数为u,物块的质量为m,弹簧的劲度系数为k,且k>$\frac{4μmg}{L}$,物块第一次到达c点时,物块的速度大小为vo,这时弹簧的弹性势能为E0,不计物块的大小,则下列说法正确的是( )| A. | 物块可能会停在CB面上某处 | |
| B. | 物块最终会做往复运动 | |
| C. | 弹簧开始具有的最大弹簧势能为$\frac{1}{2}$mv02+E0 | |
| D. | 物块克服摩擦做的功最大为$\frac{1}{2}$mv02+$\frac{1}{2}$μmgL |
8. 如图所示,在垂直纸面向里、磁感应强度为B的匀强磁场区域中,有一个均匀导线制成的单匝直角三角形线框,现用外力使线框以恒定的速度v沿垂直磁场方向向右运动,运动中线框的AB边始终与磁场右边界平行.已知AB=BC=l,线框的总电阻为R,则线框离开磁场的过程中( )
如图所示,在垂直纸面向里、磁感应强度为B的匀强磁场区域中,有一个均匀导线制成的单匝直角三角形线框,现用外力使线框以恒定的速度v沿垂直磁场方向向右运动,运动中线框的AB边始终与磁场右边界平行.已知AB=BC=l,线框的总电阻为R,则线框离开磁场的过程中( )
 如图所示,在垂直纸面向里、磁感应强度为B的匀强磁场区域中,有一个均匀导线制成的单匝直角三角形线框,现用外力使线框以恒定的速度v沿垂直磁场方向向右运动,运动中线框的AB边始终与磁场右边界平行.已知AB=BC=l,线框的总电阻为R,则线框离开磁场的过程中( )
如图所示,在垂直纸面向里、磁感应强度为B的匀强磁场区域中,有一个均匀导线制成的单匝直角三角形线框,现用外力使线框以恒定的速度v沿垂直磁场方向向右运动,运动中线框的AB边始终与磁场右边界平行.已知AB=BC=l,线框的总电阻为R,则线框离开磁场的过程中( )| A. | 线框A、B两点间的电压不变 | |
| B. | 线框的热功率与时间成正比 | |
| C. | 线框所受外力的最大值为$\frac{\sqrt{2}B{I}^{2}v}{R}$ | |
| D. | 通过线框导线横截面的电荷量为$\frac{B{I}^{2}}{2R}$ |
15. 如图所示,闭合小金属球从高h处的光滑曲面上端无初速度滚下,又沿曲面的另一侧上升,则下列说法正确的是( )
如图所示,闭合小金属球从高h处的光滑曲面上端无初速度滚下,又沿曲面的另一侧上升,则下列说法正确的是( )
 如图所示,闭合小金属球从高h处的光滑曲面上端无初速度滚下,又沿曲面的另一侧上升,则下列说法正确的是( )
如图所示,闭合小金属球从高h处的光滑曲面上端无初速度滚下,又沿曲面的另一侧上升,则下列说法正确的是( )| A. | 若是匀强磁场,球在左侧滚上的高度等于h | |
| B. | 若是匀强磁场,球在左侧滚上的高度小于h | |
| C. | 若是非匀强磁场,球在左侧滚上的高度等于h | |
| D. | 若是非匀强磁场,球在左侧滚上的高度小于h |
5.关于行星的运动,以下说法正确的是( )
| A. | .行星轨道的半长轴越长,自转周期就越大 | |
| B. | .行星轨道的半长轴越短,公转周期就越大 | |
| C. | 水星离太阳最“近“,公转周期最大 | |
| D. | 冥王星离太阳“最远”,绕太阳运动的公转周期最长 |
12.在下述现象中没有做功而使物体内能改变的是( )
| A. | 电流通过点炉丝使温度生高 | B. | 流星进入大气层运动温度升高 | ||
| C. | 铁锤打铁块使铁块温度升高 | D. | 在炉火上的水被烧开 |
9.小李家的一个水龙头拧不紧,水一滴一滴不停地滴落到地上.小李发现,第一滴水碰地的同时,第二滴水刚好从水龙头处下落.他为了测算水滴下落的平均速度,找来了秒表和卷尺.首先量出水龙头口离地面的高度h,再用秒表计时.当他听到某一水滴滴在地上声音的同时,开启秒表开始计时,并数“1”,以后每听到一声水滴声,依次数“2、3…”,一直数到“n”时,按下秒表停止计时,读出秒表的示数为t.
(1)水滴在空中运动的平均速度的表达式为$\frac{(n-1)h}{t}$;;
(2)测得h=1m当数到n=20时秒表的示数 t=8.7s,则水滴下落的平均速度为2.18m/s;
(3)小李为了进一步找出水滴下落的平均速度和下落高度的关系,又做了以下实验:找来一块挡板,让水滴落在挡板上.改变挡板和水龙头口之间的距离h,并仔细调节水龙头滴水的快慢,使得总是在前一滴水滴到挡板上的同时,后一滴水刚好开始下落.计时方法仍和上面一样.他从实验中又获得了如表所示的6组数据(连同上面的一组共有7组数据).请在图2中选取合适的坐标轴,标上数据和单位,作出相应的图象,并根据图象写出平均速度和下落高度的函数关系为${\overline{v}}^{2}=4.8h$..

(1)水滴在空中运动的平均速度的表达式为$\frac{(n-1)h}{t}$;;
(2)测得h=1m当数到n=20时秒表的示数 t=8.7s,则水滴下落的平均速度为2.18m/s;
(3)小李为了进一步找出水滴下落的平均速度和下落高度的关系,又做了以下实验:找来一块挡板,让水滴落在挡板上.改变挡板和水龙头口之间的距离h,并仔细调节水龙头滴水的快慢,使得总是在前一滴水滴到挡板上的同时,后一滴水刚好开始下落.计时方法仍和上面一样.他从实验中又获得了如表所示的6组数据(连同上面的一组共有7组数据).请在图2中选取合适的坐标轴,标上数据和单位,作出相应的图象,并根据图象写出平均速度和下落高度的函数关系为${\overline{v}}^{2}=4.8h$..
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 高度h(m) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.8 |
| 平均速度v(m/s) | 0.97 | 1.19 | 1.38 | 1.5 4 | 1.6 8 | 1.9 5 |

10.关于质点,下列说法正确的是( )
| A. | 研究刘翔在110m栏比赛中的过杆技术是否合理时,能把刘翔看作质点 | |
| B. | 在奥运会女排比赛中,陈忠和主教练在战术板上布置队员怎样跑位时,不能把女排队员看作质点 | |
| C. | 研究奥运会跳水冠军田亮的跳水动作时,能把田亮看作质点 | |
| D. | 研究乒乓球比赛中打的弧圈球时,不能把乒乓球看作质点 |