��Ŀ����
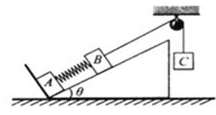
����Ŀ����ͼ��ʾ�����![]() =37�����㹻���⻬б��̶���ˮƽ�����ϣ����϶˹̶�һ�⻬�����֣�����Aͨ����������ֵ�����ϸ�������B��������ʼʱ����A��������б�棻 ��Ϊ�ʵ�����C�ӱ���A�����϶��ɾ�ֹ�ͷš���֪����A�����B�����C�������ֱ�ΪmA=2kg��mB=4kg��mC=lkg������A�����C֮��Ļ���Ħ��������=0.5��sin37��=0.6��cos37��=0.8��ȡ�������ٶ�g= 10m/s2��
=37�����㹻���⻬б��̶���ˮƽ�����ϣ����϶˹̶�һ�⻬�����֣�����Aͨ����������ֵ�����ϸ�������B��������ʼʱ����A��������б�棻 ��Ϊ�ʵ�����C�ӱ���A�����϶��ɾ�ֹ�ͷš���֪����A�����B�����C�������ֱ�ΪmA=2kg��mB=4kg��mC=lkg������A�����C֮��Ļ���Ħ��������=0.5��sin37��=0.6��cos37��=0.8��ȡ�������ٶ�g= 10m/s2��

��1�������C�ͷ�ʱ�ļ��ٶȣ�
��2����t=0ʱ���ͷ����C��ͬʱ����Ա���A��������
����t=1sʱ����A�����B�����C���ٶȴ�С����ʱ���Cδ���뱡��A����
����t=lsʱ��������ϸ�����������Cǡ��û�л��뱡��A����A�ij��ȡ�
���𰸡���1��2m/s2��2����4m/s��4m/s��2m/s����6m
��������
��1�������C����ţ�ٵڶ����ɣ�![]()
���![]()
�������ݽ��aC=2m/s2
��2�����ͷ����C��ͬʱ����Ա���A�����������ʱC�ļ��ٶ���Ϊ��б�����£���СΪaC=2m/s2
��AB���壺![]()
���a= 4m/s2
��t=1sʱ����A�����B���ٶȴ�С��vA=vB=at=4m/s��
���C���ٶȣ�vC=aCt=2m/s
����t=lsʱ��������ϸ������ʱC���µ�λ��![]() ��
��
A���ϵ�λ�ƣ�![]()
��������ϸ��ʱA�ļ��ٶȣ�![]()
���a��=8m/s2�������������
��A��C����ʱ��![]() ��
��
���t��=1s v��=4m/s
�˹�����C���µ�λ�ƣ�![]()
A��λ�ƣ�![]()
��ľ��A�ij���Ϊ��![]()

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�