题目内容
8. 如图所示,水平轨道与竖直平面内的光滑半圆形轨道平滑连接,半圆形轨道的半径R=0.40m.一轻质弹簧的左端固定在墙M上,右端连接一个质量m=0.20kg的小滑块.开始时滑块静止在P点,弹簧正好处于原长.现水平向左推滑块压缩弹簧,使弹簧具有一定的弹性势能Ep,然后释放滑块,运动到最高点A时的速度vA=3.0m/s.已知水平轨道MP部分是光滑的,滑块与水平轨道PB间的动摩擦因数μ=0.25,PB=2.0m,取g=10m/s2.求:
如图所示,水平轨道与竖直平面内的光滑半圆形轨道平滑连接,半圆形轨道的半径R=0.40m.一轻质弹簧的左端固定在墙M上,右端连接一个质量m=0.20kg的小滑块.开始时滑块静止在P点,弹簧正好处于原长.现水平向左推滑块压缩弹簧,使弹簧具有一定的弹性势能Ep,然后释放滑块,运动到最高点A时的速度vA=3.0m/s.已知水平轨道MP部分是光滑的,滑块与水平轨道PB间的动摩擦因数μ=0.25,PB=2.0m,取g=10m/s2.求:(1)滑块在圆弧轨道起点B的速度vB.
(2)滑块由A点抛出后,落地点与A点间的水平距离x.
(3)若要求滑块过圆弧轨道最高点A后,落在水平面PB段且最远不超过P点,求弹簧处于压缩状态时具有的弹性势能Ep的范围.
分析 (1)滑块从B运动到A的过程,满足机械能守恒,由此求解速度vB.
(2)滑块从A点飞出后做平抛运动,由平抛运动规律可求得水平距离x.
(3)当滑块经过圆轨道时,刚好通过最高点A时,由重力充当向心力,由牛顿第二定律A点的最小速度,从而得到弹性势能Ep的最小值.当滑块落在P点时,由平抛运动规律求出滑块通过A点的速度,由能量守恒求出弹性势能Ep的最大值,即得到弹性势能Ep的范围.
解答 解:(1)对滑块,由B到A过程,根据机械能守恒得:
$\frac{1}{2}m{v}_{B}^{2}$=$\frac{1}{2}m{v}_{A}^{2}$+2mgR
代入数据解得:vB=5 m/s
(2)滑块从A点抛出后,满足:
水平方向:x=vAt
竖直方向:2R=$\frac{1}{2}g{t}^{2}$
代入数据解得:x=1.2 m
(3)①当滑块经过圆轨道时,刚好通过最高点A,在A点 由牛顿第二定律由:
mg=m$\frac{{v}_{1}^{2}}{R}$
代入数据得最小速度为:v1=2 m/s
过A点后,做平抛运动,有:
x1=v1t,
2R=$\frac{1}{2}g{t}^{2}$
代入数据得,落地时间为:t=0.4 s
最小位移为:x1=0.8 m<1.2 m
对于全程,由功能关系得:
-μmgL=2mgR+$\frac{1}{2}m{v}_{1}^{2}$-Ep1
代入数据,得弹簧弹性势能最小值为:Ep1=3 J
②当滑块过A点后,做平抛运动,时间t=0.4 s不变,
落地点在最远位置P点 x2=v2t
带入数据得 v2=5 m/s
对于全程,由功能关系得
-μmgL=2mgR+$\frac{1}{2}m{v}_{2}^{2}$-Ep2
代入数据,得弹簧弹性势能最大值 Ep2=5.1 J
所以,弹簧的弹性势能范围为:3 J≤Ep≤5.1 J
答:(1)滑块在圆弧轨道起点B的速度vB为5m/s.
(2)滑块由A点抛出后,落地点与A点间的水平距离x是1.2m.
(3)弹簧处于压缩状态时具有的弹性势能Ep的范围为3 J≤Ep≤5.1J.
点评 本题考查平抛、动能定理及功能关系,要注意正确分析物理过程,并做好受力分析,明确能量转化的关系,选择正确的物理规律求解即可.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案| A. | 等压膨胀时,温度降低 | |
| B. | 等容降温时压强减小 | |
| C. | 压强、体积和温度都增大 | |
| D. | 压强增大时,分子密集程度和分子平均动能都减小 |
 如图所示,某人游长江,他以一定的速度面部始终垂直江岸向对岸游去.江中各处水流速度相等,他游过的路程、过江所用的时间与水速的关系是( )
如图所示,某人游长江,他以一定的速度面部始终垂直江岸向对岸游去.江中各处水流速度相等,他游过的路程、过江所用的时间与水速的关系是( )| A. | 水速大时,路程长,时间长 | B. | 水速大时,路程长,时间不变 | ||
| C. | 水速大时,路程长,时间短 | D. | 路程、时间与水速无关 |
 旅居加拿大十六岁学生温家辉,2009年在美国太空总署主办的太空移民设计赛中夺冠.温家辉的获奖设计是一个高1.6km的圆筒形建筑,命名为Asten,如图1所示,内径约1km,圆筒由一个个可以住人的环形物堆叠而成,并在电力的驱动下绕着中心轴以一定的角速度转动,从而产生“模拟重力”,使居民能在“重力”环境下生活.垂直中心轴的截面图如图2所示,圆筒的内壁正好是城市的地面,因此,生活在这座太空城市的人,站在“地面上”,跟站在地球地面上的感觉没有区别.以下说法正确的有( )
旅居加拿大十六岁学生温家辉,2009年在美国太空总署主办的太空移民设计赛中夺冠.温家辉的获奖设计是一个高1.6km的圆筒形建筑,命名为Asten,如图1所示,内径约1km,圆筒由一个个可以住人的环形物堆叠而成,并在电力的驱动下绕着中心轴以一定的角速度转动,从而产生“模拟重力”,使居民能在“重力”环境下生活.垂直中心轴的截面图如图2所示,圆筒的内壁正好是城市的地面,因此,生活在这座太空城市的人,站在“地面上”,跟站在地球地面上的感觉没有区别.以下说法正确的有( )| A. | 太空城内的居民不能运用天平准确测出质量 | |
| B. | 太空城内物体所受的“重力”一定通过垂直中心轴截面的圆心 | |
| C. | 人随太空城自转所需的向心力由人造陆地对人的支持力提供 | |
| D. | 太空城绕自己的中心轴转动的角速度越大,太空城的居民受到的“重力”越大 |
| A. | 人对地面的作用力大于地球对人的引力 | |
| B. | 地面对人的作用力大于人对地面的作用力 | |
| C. | 地面对人的作用力大于地球对人的引力 | |
| D. | 地面对人的作用力对人做了正功 |
第一步:按图(甲)所示的电路图接好电路.
第二步:把电键S打到1,移动滑动变阻器的滑片,测得多组电压表和电流表的读数如表.
| U/V | 1.42 | 1.38 | 1.32 | 1.35 | 1.18 | 1.10 |
| I/A | 0.15 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
第四步:理整仪器.
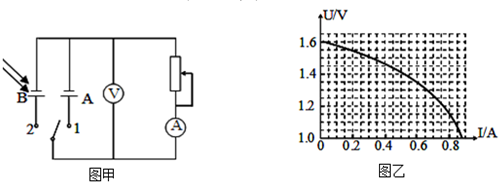
完成下列问题:
(1)在图(乙)中作出第二步实验的U-I图象,求出干电池A的电动势EA=1.52V,内电阻r=0.70Ω.
(2)在第二步中当滑动变阻器的电阻为某值时,电压表读数为1.2V,保持滑动变阻器的阻值不变把电键S打到2,则此时硅光电池B的输出功率P=0.73W.
| A. | 千克 | B. | 厘米 | C. | 米/秒 | D. | 牛顿 |
| A. | 火星和木星公转周期相等 | |
| B. | 火星和木星绕太阳运行速度的大小始终相等 | |
| C. | 火星和木星公转周期之比的平方等于它们轨道半长轴之比的立方 | |
| D. | 相同时间内,火星与太阳连线扫过的面积等与木星与太阳连线扫过的面积 |
 如图所示,在“探究功与物体速度变化的关系”的实验中:
如图所示,在“探究功与物体速度变化的关系”的实验中: