题目内容
11. 如图所示,在水平面上有一质量为m的小物块,在某时刻给它一初速度,使其沿水平面做匀减速直线运动,其依次经过A、B、C三点,最终停在O点.A、B、C三点到O点的距离分别为L1、L2、L3,小物块由A、B、C三点运动到O点所用的时间分别为t1、t2、t3.下列结论正确的是( )
如图所示,在水平面上有一质量为m的小物块,在某时刻给它一初速度,使其沿水平面做匀减速直线运动,其依次经过A、B、C三点,最终停在O点.A、B、C三点到O点的距离分别为L1、L2、L3,小物块由A、B、C三点运动到O点所用的时间分别为t1、t2、t3.下列结论正确的是( )| A. | $\frac{{L}_{1}}{{t}_{1}}$>$\frac{{L}_{2}}{{t}_{2}}$>$\frac{{L}_{3}}{{t}_{3}}$ | B. | $\frac{{L}_{1}}{{t}_{1}}$=$\frac{{L}_{2}}{{t}_{2}}$=$\frac{{L}_{3}}{{t}_{3}}$ | ||
| C. | $\frac{{L}_{1}}{{{t}_{1}}^{2}}$>$\frac{{L}_{2}}{{{t}_{2}}^{2}}$>$\frac{{L}_{3}}{{{t}_{3}}^{2}}$ | D. | $\frac{{L}_{1}}{{{t}_{1}}^{2}}$=$\frac{{L}_{2}}{{{t}_{2}}^{2}}$=$\frac{{L}_{3}}{{{t}_{3}}^{2}}$ |
分析 采用逆向思维,小球从0开始做初速度为零的匀加速直线运动,由运动学公式可判断各项是否正确.
解答 解:采用逆向思维,小球做初速度为零的匀加速直线运动,对OA、OB、OC段,根据x=$\frac{1}{2}a{t}^{2}$得,$\frac{2{L}_{1}}{{{t}_{1}}^{2}}=\frac{2{L}_{2}}{{{t}_{2}}^{2}}=\frac{2{L}_{3}}{{{t}_{3}}^{2}}$,可知$\frac{{L}_{1}}{{{t}_{1}}^{2}}=\frac{{L}_{2}}{{{t}_{2}}^{2}}=\frac{{L}_{3}}{{{t}_{3}}^{2}}$,故C错误,D正确.
A到O做匀减速直线运动,速度越来越小,可知vA>vB>vC,根据平均速度推论有:$\overline{v}=\frac{L}{t}=\frac{v}{2}$,可知$\frac{{L}_{1}}{{t}_{1}}>\frac{{L}_{2}}{{t}_{2}}>\frac{{L}_{3}}{{t}_{3}}$,故A正确,B错误.
故选:AD.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,以及掌握逆向思维在运动学中的运用,难度不大.

练习册系列答案
相关题目
19. 伽利略对自由落体运动的研究,是科学实验和逻辑推理的完美结合.伽利略先用斜面进行实验研究,获得匀变速直线运动的规律,然后将此规律合理外推至倾角为90°--自由落体的情形,如图所示.对伽利略研究过程的理解,下列说法正确的是( )
伽利略对自由落体运动的研究,是科学实验和逻辑推理的完美结合.伽利略先用斜面进行实验研究,获得匀变速直线运动的规律,然后将此规律合理外推至倾角为90°--自由落体的情形,如图所示.对伽利略研究过程的理解,下列说法正确的是( )
 伽利略对自由落体运动的研究,是科学实验和逻辑推理的完美结合.伽利略先用斜面进行实验研究,获得匀变速直线运动的规律,然后将此规律合理外推至倾角为90°--自由落体的情形,如图所示.对伽利略研究过程的理解,下列说法正确的是( )
伽利略对自由落体运动的研究,是科学实验和逻辑推理的完美结合.伽利略先用斜面进行实验研究,获得匀变速直线运动的规律,然后将此规律合理外推至倾角为90°--自由落体的情形,如图所示.对伽利略研究过程的理解,下列说法正确的是( )| A. | 图中所示的情形均为真实的实验过程 | |
| B. | 该研究方法的核心是把实验和逻辑推理结合起来 | |
| C. | 利用斜面“放大”重力的作用,使实验现象更明显 | |
| D. | 利用斜面“冲淡”重力的作用,便于测量实验数据 |
6.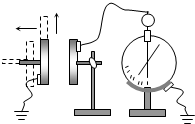 采用控制变量法探究影响平行板电容器电容的因素的实验装置如图所示,充满电的两个极板所带电荷量不变,两极板正对面积为S,极板间的距离为d,静电计指针偏角为θ.实验中,改变电容器的结构,关于可能看到的现象,下列说法正确的是( )
采用控制变量法探究影响平行板电容器电容的因素的实验装置如图所示,充满电的两个极板所带电荷量不变,两极板正对面积为S,极板间的距离为d,静电计指针偏角为θ.实验中,改变电容器的结构,关于可能看到的现象,下列说法正确的是( )
 采用控制变量法探究影响平行板电容器电容的因素的实验装置如图所示,充满电的两个极板所带电荷量不变,两极板正对面积为S,极板间的距离为d,静电计指针偏角为θ.实验中,改变电容器的结构,关于可能看到的现象,下列说法正确的是( )
采用控制变量法探究影响平行板电容器电容的因素的实验装置如图所示,充满电的两个极板所带电荷量不变,两极板正对面积为S,极板间的距离为d,静电计指针偏角为θ.实验中,改变电容器的结构,关于可能看到的现象,下列说法正确的是( )| A. | 保持S不变,增大d,则θ变小 | B. | 保持S不变,增大d,则θ不变 | ||
| C. | 保持d不变,减小S,则θ变大 | D. | 保持d不变,减小S,则θ变小 |
3. 如图所示,小球从竖直砖墙位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的物质,连续两次曝光的时间间隔为T,每块砖的厚度为d,根据图中的信息,下列判断正确的是( )
如图所示,小球从竖直砖墙位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的物质,连续两次曝光的时间间隔为T,每块砖的厚度为d,根据图中的信息,下列判断正确的是( )
 如图所示,小球从竖直砖墙位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的物质,连续两次曝光的时间间隔为T,每块砖的厚度为d,根据图中的信息,下列判断正确的是( )
如图所示,小球从竖直砖墙位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的物质,连续两次曝光的时间间隔为T,每块砖的厚度为d,根据图中的信息,下列判断正确的是( )| A. | 位置“1”是小球释放的初始位置 | B. | 小球做变加速直线运动 | ||
| C. | 小球下落的加速度为$\frac{d}{{T}^{2}}$ | D. | 小球在位置“3”的速度为$\frac{5d}{2T}$ |
20.下列说法中不正确的是( )
| A. | 只要有电荷存在,电荷周围就一定存在电场 | |
| B. | 电场是一种物质,它与其他物质一样,是不依赖我们的感觉而客观存在的东西 | |
| C. | 电荷间的相互作用是通过电场而产生的,电场最基本的特征是对处在它里面的电荷有力的作用 | |
| D. | 电场线是客观存在的 |
1.下列说法正确的有( )
| A. | 静止的物体不可能受滑动摩擦力 | |
| B. | 同一物体在地球各处所受重力大小相等,方向相同 | |
| C. | 桌面上的物块受到的支持力是由于桌面形变产生的 | |
| D. | 合力的大小必然大于其中一个分力 |
 如图所示,S处有一电子源,可向纸面内任意方向发射电子,平板MN垂直于纸面,在纸面内的长度L=9.1cm,中点O与S间的距离d=4.55cm,ON与OS连线的夹角为θ(0<θ<π),板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场,磁感应强度B=2.0×10-4T,电子质量m=9.1×10-31kg,电量e=-1.6×10-19C,不计电子重力.电子源发射速度v=1.6×106m/s的一个电子,求:该电子打在板上可能位置的区域的长度l (用含有θ的式子表示).
如图所示,S处有一电子源,可向纸面内任意方向发射电子,平板MN垂直于纸面,在纸面内的长度L=9.1cm,中点O与S间的距离d=4.55cm,ON与OS连线的夹角为θ(0<θ<π),板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场,磁感应强度B=2.0×10-4T,电子质量m=9.1×10-31kg,电量e=-1.6×10-19C,不计电子重力.电子源发射速度v=1.6×106m/s的一个电子,求:该电子打在板上可能位置的区域的长度l (用含有θ的式子表示). 质量m=1.0kg的物块A(可视为质点)与轻弹簧的上端连接,弹簧下端固定在光滑斜面底端,斜面的倾斜角θ=30°.平衡时,弹簧的压缩量为x=0.20m,此时具有的弹性势能Ep=0.50J,物块A处在O时弹簧为原长,如图所示.一质量m=1.0kg物块B(可视为质点)从距离物块A为d=2.0m处从静止开始沿斜面下滑,与物体A发生碰撞后立刻一起向下运动,但不粘连,它们到达最低点后又向上运动.求物块B向上运动到达的最高点与O的距离s.g=10m/s2.
质量m=1.0kg的物块A(可视为质点)与轻弹簧的上端连接,弹簧下端固定在光滑斜面底端,斜面的倾斜角θ=30°.平衡时,弹簧的压缩量为x=0.20m,此时具有的弹性势能Ep=0.50J,物块A处在O时弹簧为原长,如图所示.一质量m=1.0kg物块B(可视为质点)从距离物块A为d=2.0m处从静止开始沿斜面下滑,与物体A发生碰撞后立刻一起向下运动,但不粘连,它们到达最低点后又向上运动.求物块B向上运动到达的最高点与O的距离s.g=10m/s2.